题目内容
【题目】如图，在四边形ABCD中，∠B＝135°，∠C＝120°，AB＝
，BC＝
，CD＝4，则AD边的长为_____________.
【答案】2
【解析】
作AE⊥BC，DF⊥BC，构建直角△ AEB和直角△DFC，在直角三角形中求出 BE，CF，DF，从而求出EF和DG的值，进而求出AD.
解：如图：过点A、D分别作AE、DF垂直于直线BC，垂足分别为E、F，
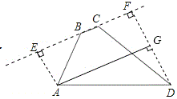
∵∠ABC=135°，
∴∠EBA=45°，
∴BE=AE,
∵AB=
,AB2=BE2+AE2，
∴BE=AE=
,
∵∠BCD=120°，
∴∠FCD=60°，∠CDF=30°
又∵CD=4，
∴CF=2，DF=2 ,
∴EF=EB+BC+CF=
=5，
过点A作AG⊥DF，垂足为G，
∴四边形AEFG是矩形，
∴GF=AE= ,AG=EF=5，则DG=DF-GF= ,
在RT△AGD中，根据勾股定理可得AD=
.
故本题答案为：2 .
练习册系列答案
阅读快车系列答案
相关题目
