Question

【题目】如图，△ABC和△BDE都是等腰直角三角形，其中∠ACB=∠BDE=90°，AC=BC，BD=ED，连接AE，点F是AE的中点，连接DF．
（1）如图1，若B、C、D共线，且AC=CD=2，求BF的长度；
（2）如图2，若A、C、F、E共线，连接CD，求证：DC= DF．

Answer 1

【答案】
（1）解：∵△ABC和△BDE都是等腰直角三角形，

∴AC=BC=CD=2，BD=DE=4，BE=4 ，AB=2 ，∠ABC=∠DBE=45°，

∴∠ABE=90°，

∴AE= = =2 ，

∵AF=EF，

∴BF= AE=

（2）证明：作AM∥DE交DF的延长线于M，交BD于N，连接CM．

∵AM∥DE，

∴∠MAE=∠DEF，

在△AFM和△EFD中，

，

∴△AFM≌△EFD，

∴AM=DE=BD，

∵∠BCE=∠BDE=90°，∠COB=∠DOE，

∴∠CBD=∠DEF=∠MAF．

在△ACM和△BCD中，

，

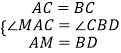∴△ACM≌△BCD，

∴∠ACM=∠BCD，CM=CD，

∴∠ACB=∠MCD=90°

∴△CDM是等腰直角三角形，

易知△BOC∽△EOD，

∴ = ，

∴ = ，

∴△BOE∽△COD，

∴∠DCO=∠OBE=45°，

∴∠FCD=∠FCM=45°，∵CM=CD，

∴FM=DF，CF⊥DM，

∴△CDF是等腰直角三角形，

∴CD= DF

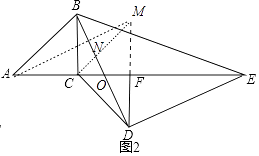
【解析】（1）证明△ABE是直角三角形，求出AB、BE，理由勾股定理求出AE，再利用直角三角形斜边中线的性质即可解决问题．（2）作AM∥DE交DF的延长线于M，交BD于N，连接CM．只要证明△CDM，△CDF都是等腰直角三角形即可解决问题；
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°．