题目内容
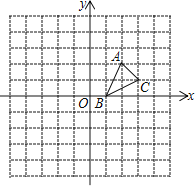
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,三个顶点的坐标分别为A(2,2)、B(1,0)、C(3,1)
(1)将△ABC关于x轴作轴对称变换得△A1B1C1,则点C1的坐标为 .
(2)将△ABC绕原点O按逆时针方向旋转90°得△A2B2C2,则点C2的坐标为 .
(3)在(1)(2)的基础上,图中的△A1B1C1、△A2B2C2是中心对称图形,对称中心的坐标为 .
(4)若以点D、A、C、B为顶点的四边形为菱形,直接写出点D的坐标为 .
【答案】(1)见解析,![]() ;(2)见解析,
;(2)见解析,![]() ;(3)
;(3)![]() ;(4)见解析,
;(4)见解析,![]()
【解析】
(1)根据网格结构找出点A、B、C关于x轴的对称点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标;
(2)根据网格结构找出点A、B、C绕点O按照逆时针旋转90°后的对应点A2、B2、的位置,然后顺次连接即可,再根据平面直角坐标系写出C2点的坐标;
(3)成中心对称图形,画出两条对应点的连线,交点就是对称中心;
(4)由图可知,菱形的边长为![]() ,即可确定D的位置.
,即可确定D的位置.
解:如下图所示,
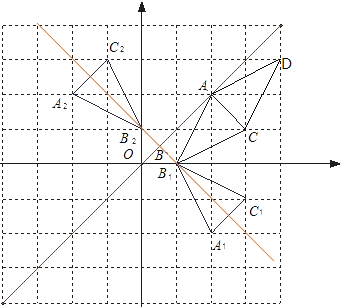
(1)点C1的坐标为:![]() ;
;
(2)点C2的坐标为:![]() ;
;
(3)对称中心的坐标为:![]() ;
;
(4)点D的坐标为:![]() .
.

【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?