题目内容
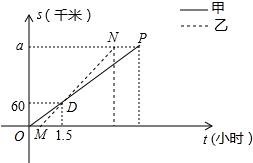 甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1h到达B地.甲车离A地的路程s1(km)与行驶的时间t(h)之间的函数关系,如图中线段OP所示;乙车离A地的路程s2(km)与行驶的时间t(h)之间的函数关系,如图中线段MN所示,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1h到达B地.甲车离A地的路程s1(km)与行驶的时间t(h)之间的函数关系,如图中线段OP所示;乙车离A地的路程s2(km)与行驶的时间t(h)之间的函数关系,如图中线段MN所示,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:(1)分别求出线段MN、OP的函数关系式;
(2)求出a的值;
(3)设甲、乙两车之间的距离为s(km),求s与甲车行驶时间t(h)的函数关系式,并求出s的最大值.
分析:(1)先确定出点M的坐标,然后利用待定系数法求一次函数解析式解答即可;
(2)先求出甲、乙的速度,然后根据乙的时间等于甲的时间减去多用的时间列出方程,解方程即可得到a的值;
(3)求出乙到达B地的时间,然后分四个阶段表示出甲、乙两车之间的距离,再根据一次函数的增减性求出各阶段时的最大值,即可得解.
(2)先求出甲、乙的速度,然后根据乙的时间等于甲的时间减去多用的时间列出方程,解方程即可得到a的值;
(3)求出乙到达B地的时间,然后分四个阶段表示出甲、乙两车之间的距离,再根据一次函数的增减性求出各阶段时的最大值,即可得解.
解答:解:(1)由题意知,M(0.5,0),
设OP的解析式为S1=k1t,
则1.5k1=60,
解得k1=40,
∴S1=40t;
设MN的解析式为S2=k2t+b,
则
,
解得
,
所以,S2=60t-30,
因此,线段OP、MN表示的函数关系式分别为:S1=40t,S2=60t-30;
(2)由(1)得甲的速度为40千米/小时,乙的速度为60千米/小时,
根据题意得,
=
-1-0.5,
解得,a=180;
(3)乙到达B地的时间为:180÷60+0.5=3.5小时,
①当0≤t≤0.5时,s=S1=40t,最大值S=40×0.5=20km;
②当0.5<t≤1.5时,s=S1-S2=40t-(60t-30)=-20t+30,没有最大值;
③当1.5<t≤3.5时,s=S2-S1=60t-30-40t=20t-30,最大值S=20×3.5-30=40;
④当3.5<t≤4.5时,s=180-S1=180-40t,没有最大值;
当t=3.5时,s的值最大为:20×3.5-30=40.
设OP的解析式为S1=k1t,
则1.5k1=60,
解得k1=40,
∴S1=40t;
设MN的解析式为S2=k2t+b,
则
|
解得
|
所以,S2=60t-30,
因此,线段OP、MN表示的函数关系式分别为:S1=40t,S2=60t-30;
(2)由(1)得甲的速度为40千米/小时,乙的速度为60千米/小时,
根据题意得,
| a |
| 60 |
| a |
| 40 |
解得,a=180;
(3)乙到达B地的时间为:180÷60+0.5=3.5小时,
①当0≤t≤0.5时,s=S1=40t,最大值S=40×0.5=20km;
②当0.5<t≤1.5时,s=S1-S2=40t-(60t-30)=-20t+30,没有最大值;
③当1.5<t≤3.5时,s=S2-S1=60t-30-40t=20t-30,最大值S=20×3.5-30=40;
④当3.5<t≤4.5时,s=180-S1=180-40t,没有最大值;
当t=3.5时,s的值最大为:20×3.5-30=40.
点评:本题考查了一次函数的应用,主要利用了待定系数法求函数解析式,行程问题,以及利用一次函数的增减性求最大值,难点在于(3)要分段讨论.

练习册系列答案
相关题目
 26、实际运用
26、实际运用 (2013•高淳县一模)甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(2013•高淳县一模)甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: 象.请结合图象信息解答下列问题:
象.请结合图象信息解答下列问题: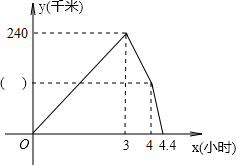 120千米,下图是两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.
120千米,下图是两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.