��Ŀ����
��ƽ��ֱ������ϵ�У��ȱ�������OAB�ı߳���2| 3 |
��1������OAB��ֱ��y=kx+b�۵�ʱ�������Aǡ�����ڵ�C��0��0������b��ֵ��
��2������OAB��ֱ��y=kx+b�۵�ʱ����C�ĺ�����Ϊm����b��m֮��ĺ�����ϵʽ����д����b=
| 1 |
| 2 |
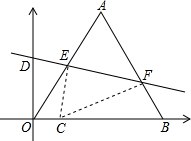
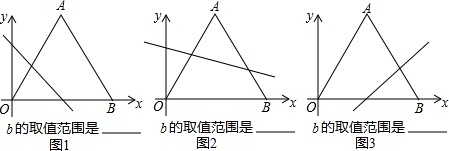
��3������OAB��ֱ��y=kx+b�۵�ʱ��������ǰ��ۺ�����ֱ�����OAB��λ�÷�Ϊ��ͼ1��ͼ2��ͼ3�������Σ�����ֱ�д��ÿ������ʱb��ȡֵ��Χ������ֱ����д��ÿ�������µĺ����ϣ���
��������1�����ݵȱ������ε����ʣ�֪�����Aǡ�����ڵ�C��0��0������ֱ�߹���B����ֱ�ߺ�y��Ľ�����M�������30���ֱ�������ε����ʼ������b��ֵ��
��2�����������ӣ���A�����ֱ��y=kx+b�ĶԳƵ�C��x���ϣ���ôAC���е���ֱ��y=kx+b�ϣ���ֱ��AC��б��Ϊ-
����AC��ֱ��y=kx+b��ֱ�����ɸ��������������õ�b��m�Ĺ�ϵʽ��������ֵ���C�����꣮
��3������Ҫ��ϣ�2���Ľ�������⣬�������濼�ǣ�
���ɣ�2���ɵõ�����m�Ķ��η��̣���C����x���ϣ���ô����m�ķ��̵ĸ����б�ʽ�ش��ڵ���0��
�ڸ���ͼ��ֱ�ߵ�λ�ã������жϳ�m��������Сֵ��Ȼ���ٴ��루2���Ľ���ʽ�н�����⣮
��2�����������ӣ���A�����ֱ��y=kx+b�ĶԳƵ�C��x���ϣ���ôAC���е���ֱ��y=kx+b�ϣ���ֱ��AC��б��Ϊ-
| 1 |
| k |
��3������Ҫ��ϣ�2���Ľ�������⣬�������濼�ǣ�
���ɣ�2���ɵõ�����m�Ķ��η��̣���C����x���ϣ���ô����m�ķ��̵ĸ����б�ʽ�ش��ڵ���0��
�ڸ���ͼ��ֱ�ߵ�λ�ã������жϳ�m��������Сֵ��Ȼ���ٴ��루2���Ľ���ʽ�н�����⣮
����⣺��1�����ݵȱ������ε����ߺ�һ�����ʣ����ʱֱ�߹���B��
��ֱ�ߺ�y��Ľ�����M��
��Rt��CBM�У���CBM=30�㣬OB=2
��
��OM=2����b=2��
��2����֪��A��
��3������֪C��m��0������AC���е�Ϊ��
��
����
��������
��
��ȥk���ã�m2+6b-12=0����b=2-
m2��
��b=
ʱ��2-
m2=
�����m=��3��
�ʣ�C1��3��0����C2��-3��0������5�֣�
��3��ͼ�٣�0��b��2��ͼ�ڣ�0��b��2��ͼ�ۣ�-6��b��0��
���ɣ��ɣ�2��֪��12-6b=m2��m2+6b-12=0��
��C����x���ϣ���m2+6b-12=0����ʵ���⣬����
��=-4��6b-12����0�����b��2��
ͼ���У���Ȼb��0����ôb��ȡֵ��Χ�ǣ�0��b��2��
ͼ���У���Ȼb��0��ͬͼ�ٿɵã�0��b��2��
ͼ���У���Ȼb��0������m��ֵ����ȡ4
����ô��
12-6b2�ܣ�4
��2����b��-6��
���-6��b��0��
��ֱ�ߺ�y��Ľ�����M��
��Rt��CBM�У���CBM=30�㣬OB=2
| 3 |
��OM=2����b=2��
��2����֪��A��
| 3 |
m+
| ||
| 2 |
| 3 |
| 2 |
��������
|
��ȥk���ã�m2+6b-12=0����b=2-
| 1 |
| 6 |
��b=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
�ʣ�C1��3��0����C2��-3��0������5�֣�
��3��ͼ�٣�0��b��2��ͼ�ڣ�0��b��2��ͼ�ۣ�-6��b��0��
���ɣ��ɣ�2��֪��12-6b=m2��m2+6b-12=0��
��C����x���ϣ���m2+6b-12=0����ʵ���⣬����
��=-4��6b-12����0�����b��2��
ͼ���У���Ȼb��0����ôb��ȡֵ��Χ�ǣ�0��b��2��
ͼ���У���Ȼb��0��ͬͼ�ٿɵã�0��b��2��
ͼ���У���Ȼb��0������m��ֵ����ȡ4
| 3 |
12-6b2�ܣ�4
| 3 |
���-6��b��0��
������������һ�κ������ۺ���Ŀ���漰��ͼ�εķ��۱任���Լ������벻��ʽ���ۺ�Ӧ�õ�֪ʶ���ѶȽϴ�

��ϰ��ϵ�д�
 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�����Ŀ
 ����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB= 18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��
18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��