Question

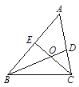
【题目】如图，在△ABC中，BD、CE分别平分∠ABC、∠ACB，∠A＝50°，则∠BOE＝__°．

Answer 1

【答案】65.

【解析】

在△ABC中，根据角平分线的定义及三角形内角和定理，先求得∠ABD+∠ACE的值，从而求得∠CBD+∠ECB的值；然后在△BOC中利用三角形内角和定理求得∠BOC度数，从而得∠BOE的度数．

∵BD、CE分别平分∠ABC和∠ACB，

∴∠ABD=∠CBD，∠ACE=∠ECB；

∵∠A+∠ABC+∠ACB=180°，

∴∠A+2∠CBD+2∠ECB=180°；

∵∠A=50°，

∴∠CBD+∠ECB=65°；

在△BOC中，

又∵∠BOC+∠CBD+∠ECB=180°，

∴∠BOC=115°．

∴∠BOE=180°-∠BOC=180°-115°=65°.

故答案为：65°．