题目内容
【题目】已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，且与双曲线y= 
交于点C（1，a）．
（1）试确定双曲线的函数表达式；
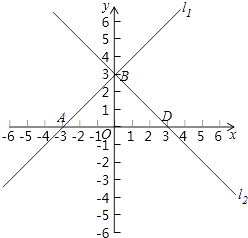
（2）将l1沿y轴翻折后，得到l2 ， 画出l2的图象，并求出l2的函数表达式；
（3）在（2）的条件下，点P是线段AC上点（不包括端点），过点P作x轴的平行线，分别交l2于点M，交双曲线于点N，求S△AMN的取值范围．
【答案】
（1）
解：令x=1代入y=x+3，
∴y=1+3=4，
∴C（1，4），
把C（1，4）代入y= 
中，
∴k=4，
∴双曲线的解析式为：y= 
（2）
解：如图所示，
设直线l2与x轴交于点D，
由题意知：A与D关于y轴对称，
∴D的坐标为（3，0），
设直线l2的解析式为：y=ax+b，
把D与B的坐标代入上式，
得： 
，
∴解得： 
，
∴直线l2的解析式为：y=﹣x+3
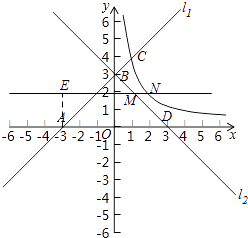
（3）
解：设M（3﹣t，t），
∵点P在线段AC上移动（不包括端点），
∴0＜t＜4，
∴PN∥x轴，
∴N的纵坐标为t，
把y=t代入y= ，
∴x= 
，
∴N的坐标为（ ，t），
∴MN= ﹣（3﹣t）= +t﹣3，
过点A作AE⊥PN于点E，
∴AE=t，
∴S△AMN= 
AEMN，
= t（ +t﹣3）
= t2﹣ 
t+2
= （t﹣ ）2+ 
，
由二次函数性质可知，当0≤t≤ 时，S△AMN随t的增大而减小，当 ＜t≤4时，S△AMN随t的增大而增大，
∴当t= 时，S△AMN可取得最小值为 ，
当t=4时，S△AMN可取得最大值为4，
∵0＜t＜4
∴ ≤S△AMN＜4
【解析】本题考查函数的综合问题，涉及待定系数法求一次函数解析式和反比例函数解析式，三角形面积等知识，由于有动点，所以难度较高，需要学生利用参数去表示相关坐标，然后求出函数关系式．（1）令x=1代入一次函数y=x+3后求出C的坐标，然后把C代入反比例函数解析式中即可求出k的值；（2）设直线l2与x轴交于D，由题意知，A与D关于y轴对称，所以可以求出D的坐标，再把B点坐标代入y=ax+b即可求出直线l2的解析式；（3）设M的纵坐标为t，由题意可得M的坐标为（3﹣t，t），N的坐标为（ ，t），进而得MN= +t﹣3，又可知在△ABM中，MN边上的高为t，所以可以求出S△AMN与t的关系式．
【考点精析】通过灵活运用确定一次函数的表达式和三角形的面积，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；三角形的面积=1/2×底×高即可以解答此题．
