题目内容
如图已知在梯形ABCD中,AD∥BC,∠A=90°,AB=8,AD=6,CD=10,P是线段AB上的一个动点, 设PB=x,△PCD的面积为y,
设PB=x,△PCD的面积为y,(1)求y与x之间的函数关系式,并写出x的取值范围.
(2)求当x为何值时,△APD∽△BPC.
(3)求当x为何值时,PC平分∠BCD.
分析:(1)过D作DE⊥BC于E,利用直角梯形的性质和勾股数易得到EC=6,而y=S梯形ABCD-S△PAD-S△PBC,然后利用梯形和三角形的面积公式计算即可y与x之间的函数关系式;
(2)根据三角形相似的判定定理得到当AP:BP=AD:BC时,Rt△APD∽Rt△BPC,即(8-x):x=6:12,即可求出x的值;
(3)过P作PH⊥DC于H,根据角平分线的判定定理得到当PH=PB时,PC平分∠BCD,则PH=x,得到△PCD的面积为y=
PH•DC=
•x•10=5x,然后和(1)中的结论建立方程关于x的方程,解方程即可.
(2)根据三角形相似的判定定理得到当AP:BP=AD:BC时,Rt△APD∽Rt△BPC,即(8-x):x=6:12,即可求出x的值;
(3)过P作PH⊥DC于H,根据角平分线的判定定理得到当PH=PB时,PC平分∠BCD,则PH=x,得到△PCD的面积为y=
| 1 |
| 2 |
| 1 |
| 2 |
解答: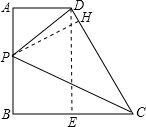 解:(1)过D作DE⊥BC于E,如图,
解:(1)过D作DE⊥BC于E,如图,
∵AD∥BC,∠A=90°,AB=8,AD=6,
∴BE=AD=6,DE=AB=8,
在Rt△DEC中,DC=10,
∴EC=6,
∴BC=6+6=12,
而PB=x,则PA=8-x,
∴y=S梯形ABCD-S△PAD-S△PBC=
•(6+12)•8-
•6•(8-x)-
•x•12=-3x+48(0≤x≤8);
(2)当AP:BP=AD:BC时,Rt△APD∽Rt△BPC,
∴(8-x):x=6:12,
解得x=
.
∴当x为
时,△APD∽△BPC;
(3)过P作PH⊥DC于H,如图,
当PH=PB时,PC平分∠BCD,
∴PH=x,
∴y=
PH•DC=
•x•10=5x,
而y=-3x+48(0≤x≤8),
∴5x=-3x+48,
解得x=6.
∴当x为6时,PC平分∠BCD.
 解:(1)过D作DE⊥BC于E,如图,
解:(1)过D作DE⊥BC于E,如图,∵AD∥BC,∠A=90°,AB=8,AD=6,
∴BE=AD=6,DE=AB=8,
在Rt△DEC中,DC=10,
∴EC=6,
∴BC=6+6=12,
而PB=x,则PA=8-x,
∴y=S梯形ABCD-S△PAD-S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)当AP:BP=AD:BC时,Rt△APD∽Rt△BPC,
∴(8-x):x=6:12,
解得x=
| 16 |
| 3 |
∴当x为
| 16 |
| 3 |
(3)过P作PH⊥DC于H,如图,
当PH=PB时,PC平分∠BCD,
∴PH=x,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
而y=-3x+48(0≤x≤8),
∴5x=-3x+48,
解得x=6.
∴当x为6时,PC平分∠BCD.
点评:本题考查了三角形相似的判定定理:有两组对应边的比相等,且它们的夹角也对应相等,则这两个三角形相似.也考查了直角梯形的性质、角平分线的判定以及梯形与三角形的面积公式.

练习册系列答案
相关题目
 如图,已知在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
如图,已知在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°. 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是