题目内容
如图,电线杆AB铅垂的竖立在坡角为30°的山坡上,太阳光线与水平线成60°时,电线杆AB的影子BC长为4米.(1)求电线杆AB的长;
(2)同一时刻与AB高度相等的电线杆DE铅垂的竖立在平地上,电线杆DE的影子EF都在平地上,求影子EF的长.

【答案】分析:此题是把实际问题转化为解直角三角形问题,
(1)先由已知作图(如图),由已知得,AE⊥ED,∠AED=60°则得:∠A=30°,再由已知得∠F=30°,可得∠EBF=60°,则∠ABC=∠EBF=60°,那么∠ACB=90°,根据直角三角形的性质可求出AB.
(2)先由已知作图(如图),得到,DE=8,DE⊥EF,∠DFE=60°,可根据直角三角形的性质求出EF,即影子EF的长.
解答: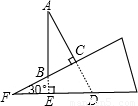 解:(1)由已知得:AE⊥ED,∠ADE=60°,
解:(1)由已知得:AE⊥ED,∠ADE=60°,
∴∠A=30°,
又∠F=30°,
∴∠EBF=60°,
∴∠ABC=60°,
∴∠ACB=90°,
∴根据直角三角形的性质得:
AB=2BC=2×4=8,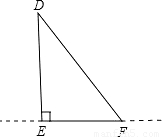
答:电线杆AB的长为8米.
(2)由已知,DE⊥EF,∠DFE=60°,DE=8,
∴在直角三角形DEF中,
EF=DE•cot60°=8×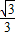 =
=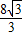 ,
,
答:影子EF的长为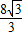 米.
米.
点评:此题考查的知识点是解直角三角形的应用问题,解答此题的关键是把实际问题转化为解直角三角形问题,(1)由已知得出直角三角形ABC,根据直角三角形的性质求出AB.(2)根据三角函数求出EF.
(1)先由已知作图(如图),由已知得,AE⊥ED,∠AED=60°则得:∠A=30°,再由已知得∠F=30°,可得∠EBF=60°,则∠ABC=∠EBF=60°,那么∠ACB=90°,根据直角三角形的性质可求出AB.
(2)先由已知作图(如图),得到,DE=8,DE⊥EF,∠DFE=60°,可根据直角三角形的性质求出EF,即影子EF的长.
解答:
 解:(1)由已知得:AE⊥ED,∠ADE=60°,
解:(1)由已知得:AE⊥ED,∠ADE=60°,∴∠A=30°,
又∠F=30°,
∴∠EBF=60°,
∴∠ABC=60°,
∴∠ACB=90°,
∴根据直角三角形的性质得:
AB=2BC=2×4=8,

答:电线杆AB的长为8米.
(2)由已知,DE⊥EF,∠DFE=60°,DE=8,
∴在直角三角形DEF中,
EF=DE•cot60°=8×
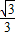 =
=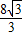 ,
,答:影子EF的长为
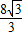 米.
米.点评:此题考查的知识点是解直角三角形的应用问题,解答此题的关键是把实际问题转化为解直角三角形问题,(1)由已知得出直角三角形ABC,根据直角三角形的性质求出AB.(2)根据三角函数求出EF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 影子BC长为4米.
影子BC长为4米. (2013•本溪二模)如图,电线杆AB铅垂地矗立在坡角是15°的山坡上,太阳光与山坡成∠ACB=60°时,电线杆AB在山坡上的影子AC长8米.求电线杆AB的长.
(2013•本溪二模)如图,电线杆AB铅垂地矗立在坡角是15°的山坡上,太阳光与山坡成∠ACB=60°时,电线杆AB在山坡上的影子AC长8米.求电线杆AB的长. 影子BC长为4米.
影子BC长为4米. 如图,电线杆AB铅垂地矗立在坡角是15°的山坡上,太阳光与山坡成∠ACB=60°时,电线杆AB在山坡上的影子AC长8米.求电线杆AB的长.
如图,电线杆AB铅垂地矗立在坡角是15°的山坡上,太阳光与山坡成∠ACB=60°时,电线杆AB在山坡上的影子AC长8米.求电线杆AB的长.