题目内容
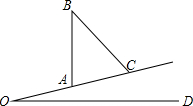 (2013•本溪二模)如图,电线杆AB铅垂地矗立在坡角是15°的山坡上,太阳光与山坡成∠ACB=60°时,电线杆AB在山坡上的影子AC长8米.求电线杆AB的长.
(2013•本溪二模)如图,电线杆AB铅垂地矗立在坡角是15°的山坡上,太阳光与山坡成∠ACB=60°时,电线杆AB在山坡上的影子AC长8米.求电线杆AB的长.分析:过点C作CE⊥AB于点E,过点A作AF⊥BC于点F,先确定∠B的度数,在Rt△ACF中求出AF,在Rt△ABF中求出AB即可.
解答:解:过点C作CE⊥AB于点E,过点A作AF⊥BC于点F,
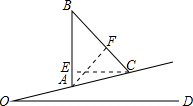
则CE∥OD,
∴∠COD=∠ACE=15°,
∴∠ECB=∠ACB-∠ACE=45°,
∴∠B=45°,
在Rt△ACF中,AC=8米,∠ACF=60°,
∴AF=ACsin∠ACF=ACsin60°=4
米,
在Rt△ABF中,AB=
AF=4
米.
答:电线杆AB的长为4
米.

则CE∥OD,
∴∠COD=∠ACE=15°,
∴∠ECB=∠ACB-∠ACE=45°,
∴∠B=45°,
在Rt△ACF中,AC=8米,∠ACF=60°,
∴AF=ACsin∠ACF=ACsin60°=4
| 3 |
在Rt△ABF中,AB=
| 2 |
| 6 |
答:电线杆AB的长为4
| 6 |
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,要求同学们能利用锐角三角函数及已知线段表示出线段的长度.

练习册系列答案
相关题目
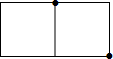 (2013•本溪二模)在1×2的正方形网格格点上放三枚棋子,按如图所示位置已放置了两枚棋子,若第三枚棋子随机放在其他格点上,则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为( )
(2013•本溪二模)在1×2的正方形网格格点上放三枚棋子,按如图所示位置已放置了两枚棋子,若第三枚棋子随机放在其他格点上,则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为( )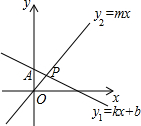 (2013•本溪二模)如图,直线y1=kx+b与直线y2=mx交于点P(1,m),则不等式mx>kx+b的解集是
(2013•本溪二模)如图,直线y1=kx+b与直线y2=mx交于点P(1,m),则不等式mx>kx+b的解集是