题目内容
已知:如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P为△ABC内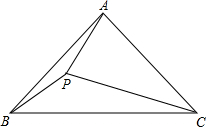 部一点,且PC=AC,∠PCA=120°-α.
部一点,且PC=AC,∠PCA=120°-α.
①用含α的代数式表示∠APC;
②求证:∠BAP=∠PCB;
③求∠PBC的度数.
 部一点,且PC=AC,∠PCA=120°-α.
部一点,且PC=AC,∠PCA=120°-α.①用含α的代数式表示∠APC;
②求证:∠BAP=∠PCB;
③求∠PBC的度数.
分析:①在三角形APC中,因为PC=AC,推出∠CPA=∠CAP,因为∠CAP+∠CPA+∠ACP=180°,推出∠CPA=∠CAP=(180°-∠ACP)÷2=(60°+α)÷2=30°+
,
②由①所推出的结论,可知∠BAP=∠BAC-∠CAP=α-(30°+
)=
-30°,在三角形ABC中,∠BCA=∠ABC=(180-a)÷2=90°-
,∠PCB=∠BCA-∠ACP=90-
-(120°-α)=
-30°,所以∠BAP=∠PC,
③分别延长CP、AP交BC于F 点,交AB于E点,由∠BAP=∠PCB,可得A,E,F,C四点共圆,得∠EFB=α,所以可得BF=EF,EF=PF,即BF=PF,又由∠AFC=∠ABC+∠BAF=90°-
+
-30°=60°,即得∠PBC=∠BPF=30°.
| α |
| 2 |
②由①所推出的结论,可知∠BAP=∠BAC-∠CAP=α-(30°+
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
③分别延长CP、AP交BC于F 点,交AB于E点,由∠BAP=∠PCB,可得A,E,F,C四点共圆,得∠EFB=α,所以可得BF=EF,EF=PF,即BF=PF,又由∠AFC=∠ABC+∠BAF=90°-
| α |
| 2 |
| α |
| 2 |
解答: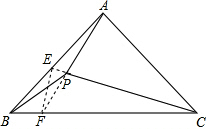 ①解:∵AB=AC,∠BAC=α,PC=AC,
①解:∵AB=AC,∠BAC=α,PC=AC,
∴∠CPA=∠CAP,∠BCA=∠ABC,
∵∠CAP+∠CPA+∠ACP=180°,
∴∠CPA=∠CAP=(180°-∠ACP)÷2=(60°+α)÷2=30°+
,
②证明:∵∠BAP=∠BAC-∠CAP,∠BAC=α,∠CAP=30°+
,
∴∠BAP=∠BAC-∠CAP=α-(30°+
)=
-30°,
∴∠BCA=∠ABC=(180-a)÷2=90°-
,
∴∠PCB=∠BCA-∠ACP=90-
-(120°-α)=
-30°,
∴∠BAP=∠PCB,
③解:分别延长CP、AP交AB于E点,交BC于F点,
∵∠BAP=∠PCB,
∴∠PFB=∠PEB,
∴A,E,F,C四点共圆,
∴∠EFB=∠BAC=α,∠EFA=∠ECA,∠FEC=∠CAF,
∴BF=EF,EF=PF,
∴BF=PF
∴∠AFC=∠ABC+∠BAF=90°-
+
-30°=60°,
∴∠PBC=∠BPF=30°.
 ①解:∵AB=AC,∠BAC=α,PC=AC,
①解:∵AB=AC,∠BAC=α,PC=AC,∴∠CPA=∠CAP,∠BCA=∠ABC,
∵∠CAP+∠CPA+∠ACP=180°,
∴∠CPA=∠CAP=(180°-∠ACP)÷2=(60°+α)÷2=30°+
| α |
| 2 |
②证明:∵∠BAP=∠BAC-∠CAP,∠BAC=α,∠CAP=30°+
| α |
| 2 |
∴∠BAP=∠BAC-∠CAP=α-(30°+
| α |
| 2 |
| α |
| 2 |
∴∠BCA=∠ABC=(180-a)÷2=90°-
| α |
| 2 |
∴∠PCB=∠BCA-∠ACP=90-
| α |
| 2 |
| α |
| 2 |
∴∠BAP=∠PCB,
③解:分别延长CP、AP交AB于E点,交BC于F点,
∵∠BAP=∠PCB,
∴∠PFB=∠PEB,
∴A,E,F,C四点共圆,
∴∠EFB=∠BAC=α,∠EFA=∠ECA,∠FEC=∠CAF,
∴BF=EF,EF=PF,
∴BF=PF
∴∠AFC=∠ABC+∠BAF=90°-
| α |
| 2 |
| α |
| 2 |
∴∠PBC=∠BPF=30°.
点评:本题主要考查等边三角形的性质,三角形内角和定理,关键在于熟练运用相关的性质定理,熟练角之间的数量转换,正确作出辅助线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,