题目内容
 如图所示,在等腰梯形ABCD中,AD∥BC,AD=DC,AB⊥AC,则∠BAD的度数为
如图所示,在等腰梯形ABCD中,AD∥BC,AD=DC,AB⊥AC,则∠BAD的度数为
- A.120°
- B.119°
- C.121°
- D.以上答案均不对
A
分析:由题中已知条件可证△DAC为等腰三角形,又AD∥BC∠B=∠C,从而得到∠B=2∠ACB,即∠ACB=∠30°,又因为∠BAC=90°,所以∠BAD=120°.
解答:∵在等腰梯形ABCD中,AD∥BC,AD=DC
∴∠DAC=∠ACB=∠DCA
∵AB=DC
∴∠B=∠DCB
∴∠ACB= ∠B
∠B
∵AB⊥AC
∴∠ACB=∠30°
∵∠BAD=∠BAC+∠CAD=90°+30°=120°
故选A.
点评:此题主要考查学生对等腰梯形的性质及角平分线等知识点的掌握情况.
分析:由题中已知条件可证△DAC为等腰三角形,又AD∥BC∠B=∠C,从而得到∠B=2∠ACB,即∠ACB=∠30°,又因为∠BAC=90°,所以∠BAD=120°.
解答:∵在等腰梯形ABCD中,AD∥BC,AD=DC
∴∠DAC=∠ACB=∠DCA
∵AB=DC
∴∠B=∠DCB
∴∠ACB=
 ∠B
∠B∵AB⊥AC
∴∠ACB=∠30°
∵∠BAD=∠BAC+∠CAD=90°+30°=120°
故选A.
点评:此题主要考查学生对等腰梯形的性质及角平分线等知识点的掌握情况.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且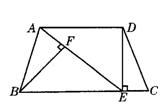 1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE.
1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE. 48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.
48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.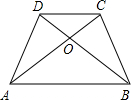 如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为
如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为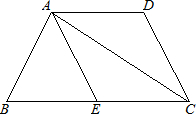 如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°
如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°