题目内容
48、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，DE⊥BC于E，BF⊥AE于F，AE=BE．请你判断线段BF与图形中哪条线段相等，先写出你的猜想，再加以证明．分析：首先可证明△FAB≌△EDC（AAS），则可得BF=DE．
解答：证明：BF=DE．
∵AE=BE，
∴∠ABE=∠EAB．
∵四边形ABCD是等腰梯形，
∴∠ABC=∠C，
∴∠EAB=∠C，
又∵DE⊥BC，BF⊥AE，
∴∠AFB=∠DEC=90°．
又∵AB=CD，
∴△FAB≌△EDC（AAS）．
∴BF=DE．
BF=DE．∵AE=BE，
∴∠ABE=∠EAB．
∵四边形ABCD是等腰梯形，
∴∠ABC=∠C，
∴∠EAB=∠C，
又∵DE⊥BC，BF⊥AE，
∴∠AFB=∠DEC=90°．
又∵AB=CD，
∴△FAB≌△EDC（AAS）．
∴BF=DE．
点评：此题主要考查三角形全等的判定方法．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
25、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，点P为BC边上任意一点，且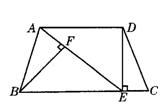
1、如图所示，在等腰梯形ABCD中，AD∥BC，DE⊥BC于点E，BF⊥AE于点F，请你添加一个条件，使△ABF≌△CDE．
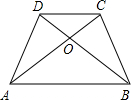如图所示，在等腰梯形ABCD中，AB∥CD，若AB+CD=4，并且∠AOB=120°，则该等腰梯形的面积为
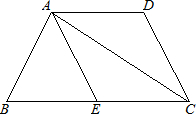如图所示，在等腰梯形ABCD中，AD∥BC，过A作腰CD的平行线，AE∥CD，AB=AD=DC，∠B=60°