题目内容
⊙O的半径为10,弦AB的长为10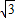 ,若以O为圆心,r为半径的圆与弦AB有两个交点,则r的取值范围是 .
,若以O为圆心,r为半径的圆与弦AB有两个交点,则r的取值范围是 .
【答案】分析:连接OB.根据勾股定理和垂径定理求解,结合图象得出r的取值范围.
解答: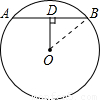 解:连接OB.
解:连接OB.
在Rt△ODB中,BD=5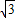 cm,OB=10cm.
cm,OB=10cm.
由勾股定理得
DO=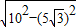 =5,
=5,
∴以O为圆心,r为半径的圆与弦AB有两个交点,DO>5,
即r>5,
∵⊙O的半径为10,
∴r的取值范围是:5<r≤10.
故答案为:5<r≤10.
点评:此题考查了直线与圆的位置关系以及垂径定理,利用勾股定理解直角三角形的能力,用垂径定理求出DO的最短长度是解题关键.
解答:
 解:连接OB.
解:连接OB.在Rt△ODB中,BD=5
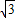 cm,OB=10cm.
cm,OB=10cm.由勾股定理得
DO=
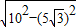 =5,
=5,∴以O为圆心,r为半径的圆与弦AB有两个交点,DO>5,
即r>5,
∵⊙O的半径为10,
∴r的取值范围是:5<r≤10.
故答案为:5<r≤10.
点评:此题考查了直线与圆的位置关系以及垂径定理,利用勾股定理解直角三角形的能力,用垂径定理求出DO的最短长度是解题关键.

练习册系列答案
相关题目
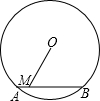 如图,已知⊙O的半径为10,弦AB=12,M是AB上任意一点,则线段OM的长可能是( )
如图,已知⊙O的半径为10,弦AB=12,M是AB上任意一点,则线段OM的长可能是( )| A、5 | B、7 | C、9 | D、11 |