��Ŀ����
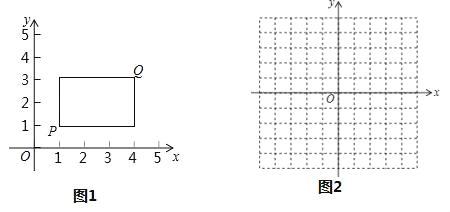
����Ŀ����ƽ��ֱ������ϵxOy�У���P������Ϊ��x1��y1������Q������Ϊ��x2��y2������x1��x2��y1��y2����P��QΪij�����ε��������㣬�Ҹþ��εı߾���ij�������ᴹֱ����Ƹþ���Ϊ��P��Q�ġ���ؾ��Ρ�����ͼΪ��P��Q�ġ���ؾ��Ρ�ʾ��ͼ��
��1����֪��A������Ϊ��1��0����
������B������Ϊ��3��1�������A��B�ġ���ؾ��Ρ��������
�ڵ�C��ֱ��x=3�ϣ�����A��C�ġ���ؾ��Ρ�Ϊ�����Σ���ֱ��AC�ı���ʽ��
��2��������RSKT����R������Ϊ��-1��1����K������Ϊ��2��-2������M������Ϊ��m��3��������������RSKT���ϴ���һ��N��ʹ�õ�M��N�ġ���ؾ��Ρ�Ϊ�����Σ���m��ȡֵ��Χ��
���𰸡���1����2����y=x��1��y=��x+1����2��1��m��7��0��m��6
�����������������
��1��������ؾ��εĶ����֪��Ҫ��A��B����ؾ����������AB��Ϊ�Խ��ߣ�����A��B��������꼴������þ��εĵ���ߵij��ȣ�����������þ��ε������
���ɶ����֪��AC��Ϊ�����εĶԽ��ߣ�����AC��x��ļнDZ�Ϊ45�㣬��ֱ��AC�Ľ���ʽΪ��y=kx+b���ɴ˿�֪k=��1���٣�1��0������y=kx+b���������b��ֵ��
��2���ɶ����֪��MN��Ϊ��ؾ��εĶԽ��ߣ�������ؾ��ε�Ϊ�����Σ���ֱ��MN��x��ļн�Ϊ45�㣬����ֱ��ƽ�п������m�ķ�Χ��
�����������1���١�A��1��0����B��3��1��
�ɶ����֪����A��B������ؾ������ĵ���߷ֱ�Ϊ2��1��
���A��B������ؾ����������Ϊ2��1=2��
���ɶ����֪��AC�ǵ�A��C������ؾ������ĶԽ��ߣ�
�֡ߵ�A��C������ؾ�����Ϊ������
��ֱ��AC��x��ļн�Ϊ45����
��ֱ��AC�Ľ���Ϊ��y=x+m��y=��x+n
�ѣ�1��0���ֱ�y=x+m��
��m=��1��
��ֱ��AC�Ľ���Ϊ��y=x��1��
�ѣ�1��0������y=��x+n��
��n=1��
��y=��x+1��
��������������A��C������ؾ�����Ϊ�����Σ�ֱ��AC�ı���ʽΪy=x��1��y=��x+1��
��2����ֱ��MN�Ľ���ʽΪy=kx+b��
�ߵ�M��N������ؾ�����Ϊ�����Σ�
���ɶ����֪��ֱ��MN��x��ļн�Ϊ45����
��k=��1��
�ߵ�N�������α��ϣ�
�൱ֱ��MN���������н���ʱ����M��N������ؾ�����Ϊ�����Σ�
��k=1ʱ��
����R��K��ֱ����ֱ��MNƽ�У�
����-1,1���ͣ�2��-2���ֱ����y=x+b
��b=2 ��b=-4
��M��m��3������y=x+2��y=x-4��
��m=1 m=7
��1��m��7��
��k=��1ʱ����(-1,-2) (2,1)����y=��x+b��
��b=-3 b=3��
��M��m��3������y=-x-3��y=-x+3��
��m=0 m=6
��0��m��6��
��������������M��N������ؾ�����Ϊ������ʱ��m��ȡֵ��Χ�ǣ�1��m��7��0��m��6