题目内容
【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(![]() )的长是方程
)的长是方程![]() 的两个根.
的两个根.
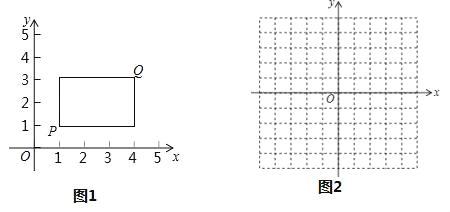
(1)如图,求点A的坐标;
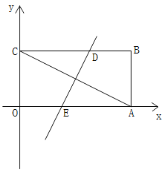
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
【答案】(1)(8,0);(2)![]() ;(3)存在点
;(3)存在点![]() 或
或![]() 或
或![]() ,使以点A、B、P、Q为顶点的四边形是平行四边形.
,使以点A、B、P、Q为顶点的四边形是平行四边形.
【解析】
(1)通过解一元二次方程可求出OA的长,结合点A在x轴正半轴可得出点A的坐标;
(2)连接CE,设OE=m,则AE=CE=8-m,在Rt△OCE中,利用勾股定理可求出m的值,进而可得出点E的坐标,同理可得出点D的坐标,根据点D,E的坐标,利用待定系数法可求出直线DE的解析式;
(3)根据点A,C的坐标,利用待定系数法可求出直线AC的解析式,设点P的坐标为(a,2a-6),点Q的坐标为(c,-![]() c+4),分AB为边和AB为对角线两种情况考虑:①当AB为边时,利用平行四边形的性质可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论;②当AB为对角线时,利用平行四边形的对角线互相平分,可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论.综上,此题得解.
c+4),分AB为边和AB为对角线两种情况考虑:①当AB为边时,利用平行四边形的性质可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论;②当AB为对角线时,利用平行四边形的对角线互相平分,可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论.综上,此题得解.
(1)解方程x2-12x+32=0,得:x1=4,x2=8.
∵OA、OC的长是方程x2-12x+32=0的两个根,且OA>OC,点A在x轴正半轴上,
∴点A的坐标为(8,0).
(2)连接CE,如图4所示.

由(1)可得:点C的坐标为(0,4),点B的坐标为(8,4).
设OE=m,则AE=CE=8-m.
在Rt△OCE中,∠COE=90°,OC=4,OE=m,
∴CE2=OC2+OE2,即(8-m)2=42+m2,
解得:m=3,
∴OE=3,
∴点E的坐标为(3,0).
同理,可求出BD=3,
∴点D的坐标为(5,4).
设直线DE解析式为:![]()
![]()
∴![]()
∴直线DE解析式为:![]()
(3)∵点A的坐标为(8,0),点C的坐标为(0,4),点B的坐标为(8,4),
∴直线AC的解析式为y=-![]() x+4,AB=4.
x+4,AB=4.
设点P的坐标为(a,2a-6),点Q的坐标为(c,-![]() c+4).
c+4).
分两种情况考虑,如图5所示:
①当AB为边时,  ,
,
解得:c1=![]() ,c2=
,c2=![]() ,
,
∴点Q1的坐标为(![]() ,
,![]() ),点Q2的坐标为(
),点Q2的坐标为(![]() ,
,![]() );
);
②当AB为对角线时, ,
,
解得: ,
,
∴点Q3的坐标为(![]() ,-
,- ![]() ).
).
综上,存在点![]() 或
或![]() 或
或![]() ,使以点A、B、P、Q为顶点的四边形是平行四边形
,使以点A、B、P、Q为顶点的四边形是平行四边形


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案