题目内容
若关于x的一元二 次方程x2+(m+1)x+m+4=0的两实根的平方和为2,求m的值.
解:设方程的两根x1,x2,那么x1+x2=(m+1),x1·x2=m+4,
∴![]() +
+![]() =(x1+x2)2-2x1x2=(m+1)2-2(m+4)=2.
=(x1+x2)2-2x1x2=(m+1)2-2(m+4)=2.
即m2=9,解得m=3.
答:m的值是3.
请把上达解答过程的钻误或不完整之处,写在横线上,并给出正确解答.
答:错误或不完整之处有:________.
答案:
解析:
提示:
解析:
|
解答:设方程两实根为x1,x2,则x1+x2=-(m+1),x1·x2=m+4. ∴ ∴m2=9,解得m=±3. 当m=3时,Δ=16-28<0,方程无实根,故m≠3. 当m=-3时Δ=0,方程有根. ∴m的值为-3. |
提示:
|
名师导引:这是一道查找解题过程是否错误的阅读理解题.命题者有意设计学生易出错的地方,在利用根与系数的关系解题时,学生易忽视方程存在实数根的前提条件:Δ≥0,因此本题错误或不完全之处有:①x1+x2=m+1;②m=3;③没有用判别式判定方程有无实根. |

练习册系列答案
相关题目
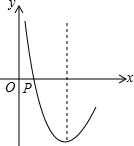 二次函数y=x2-6x+n的部分图象如图所示,若关于x的一元二次方程x2-6x+n=0的一个解为1=1,则另一个解x2( )
二次函数y=x2-6x+n的部分图象如图所示,若关于x的一元二次方程x2-6x+n=0的一个解为1=1,则另一个解x2( ) (2012•营口)二次函数y=x2-6x+n的部分图象如图所示,若关于x的一元二次方程x2-6x+n=0的一个解为x1=1,则另一个解x2=
(2012•营口)二次函数y=x2-6x+n的部分图象如图所示,若关于x的一元二次方程x2-6x+n=0的一个解为x1=1,则另一个解x2=