题目内容
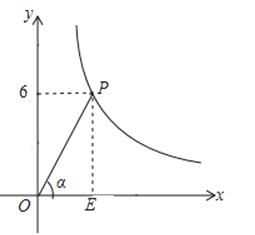
【题目】在平面直角坐标系中,点P(m,6)在第一象限,且P是反比例函数y=![]() (k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
(k>0)图象上的一点,OP与x轴正半轴的夹角α的正弦值满足:5sin2α﹣7sinα+2.4=0,求m的值及此反比例函数的解析式.
【答案】解:过点P作PE⊥x轴于点E,则可得PE=6,0E=m,
∵5sin2α﹣7sinα+2.4=0,
∴![]() ,
,
∴![]() 或
或![]() ,
,
当![]() 时,则sinα=
时,则sinα=![]()
∴OP=10,
在RT△POE中,OE=![]() =8,
=8,
∴m=8,此时,k=6×8=48,
∴![]() ;
;
当![]() 时,则sinα=
时,则sinα=![]()
∴OP=![]() ,由勾股定理得:m=
,由勾股定理得:m=![]() ,此时,k=6×4.5=27,
,此时,k=6×4.5=27,
∴![]() .
.
【解析】由5sin2α﹣7sinα+2.4=0,变形为![]() , 从而得出
, 从而得出![]() 或
或![]() ;过点P作PE⊥x轴于点E,则可得PE=6,0E=m,在Rt△POE中根据
;过点P作PE⊥x轴于点E,则可得PE=6,0E=m,在Rt△POE中根据![]() 或
或![]() , 求出OP,继而根据勾股定理求得m的值,然后根据待定系数法即可求得反比例函数的解析式.
, 求出OP,继而根据勾股定理求得m的值,然后根据待定系数法即可求得反比例函数的解析式.
【考点精析】根据题目的已知条件,利用反比例函数的性质的相关知识可以得到问题的答案,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

练习册系列答案
相关题目