题目内容
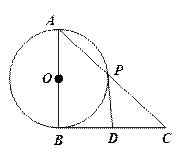
如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() 垂足为
垂足为![]()
![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() 求
求![]() 的长.
的长.

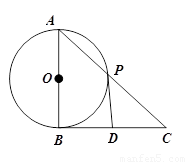
解:(1)证明:连结OC,由DC是
切线得![]() 又
又![]() ,
,
∴AD∥OC,∴∠DAC=∠ACO.
又由![]() 得∠BAC=∠ACO,
得∠BAC=∠ACO,
∴∠DAC=∠BAC. 即![]() 平分
平分![]()
(2)解: ![]() 为直径,∴
为直径,∴![]()
又∵∠BAC=∠BEC,
∴BC=AB·sin∠BAC=AB·sin∠BEC=6.
∴AC=![]() .
.
又∵∠DAC=∠BAC=∠BEC,且![]() ,
,
∴CD=AC·sin∠DAC= AC·sin∠BEC=![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
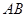 是
是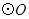 的直径,
的直径,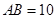 ,
, 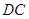 切
切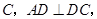 垂足为
垂足为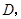
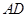 交
交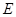 .
.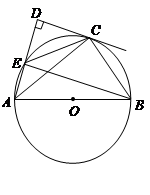
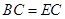 ;
; , 求
, 求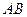 是
是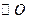 的直径,
的直径,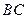 切
切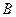 ,
,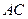 交
交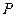 ,
,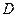 为
为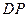 .
.
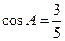 ,
, 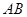 是
是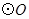 的直径,
的直径,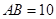 ,
, 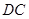 切
切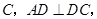 垂足为
垂足为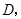
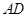 交
交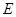 .
.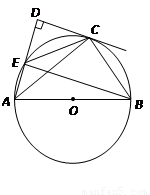
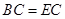 ;
;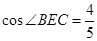 , 求
, 求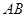 是
是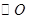 的直径,
的直径,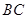 切
切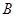 ,
, 交
交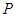 ,
,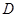 为
为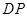 .
.
 ,
,