题目内容
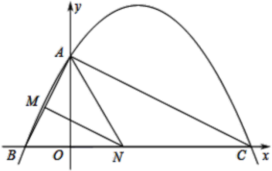
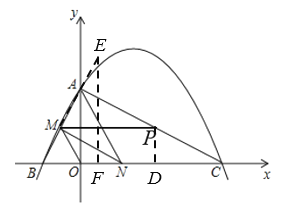
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0)、点C(8,0)两点,与y轴交于点A.
(1)求二次函数的表达式;
(2)连接AC、AB,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,线段AC上有一动点P,连接PM,求PM+![]() PC的值最小时,点P的坐标.
PC的值最小时,点P的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2) N(3,0); (3) P(1,
x+4;(2) N(3,0); (3) P(1,![]() ) .
) .
【解析】
(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)过点PD⊥x轴于点D,点E为M关于AC的对称点,作EF⊥x轴于点F,则PM+![]() PC的最小值即为EF的长.求出直线AC的解析式,并证明
PC的最小值即为EF的长.求出直线AC的解析式,并证明![]() ,再由(2)知
,再由(2)知![]() ,利用中点公式可得E的坐标,再将点E的横坐标代入直线AC,从而得解.
,利用中点公式可得E的坐标,再将点E的横坐标代入直线AC,从而得解.
(1)将点B,点C的坐标分别代入y=ax2+bx+4可得,
![]()
解得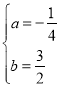 ,
,
∴二次函数的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设点N的坐标为(n,0)(﹣2<n<8),则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣![]() x2+
x2+![]() x+4中,令x=0,可解得y=4,
x+4中,令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=![]() BNOA=
BNOA=![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴![]()
∴![]()
∴![]()
∵﹣![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)如图,过点PD⊥x轴于点D,点E为M关于AC的对称点,作EF⊥x轴于点F,
![]() ,易得
,易得![]() ,当E、P、D三点共线时,可知PM+
,当E、P、D三点共线时,可知PM+![]() PC的最小值即为EF的长.
PC的最小值即为EF的长.
由(2)可得M(-1,2),
由A(0,4),B(-2,0),C(8,0),得直线AC: ![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
即![]() 是直角三角形,且
是直角三角形,且![]() ,
,
∵M,E关于AC对称,
∴A(0,4)是ME的中点,由中点坐标公式得![]() ,
,
∴点P横坐标是1,代入![]() ,得y=
,得y=![]() ,
,
则P(1,![]() ) .
) .

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案