题目内容
【题目】如图,直线y=ax+b与反比例函数y= ![]() (x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点. 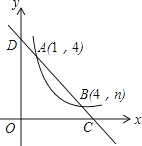
(1)m= , n=;若M(x1 , y1),N(x2 , y2)是反比例函数图象上两点,且0<x1<x2 , 则y1y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
【答案】
(1)4;1;>
(2)
解:设过C、D点的直线解析式为y=kx+b,
∵直线CD过点A(1,4)、B(4,1)两点,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线CD的解析式为y=﹣x+5.
设点P的坐标为(t,﹣t+5),
∴|t|=|﹣t+5|,
解得:t= ![]() .
.
∴点P的坐标为( ![]() ,
, ![]() ).
).
【解析】解:(1)∵反比例函数y= ![]() (x>0)的图象过点A(1,4),
(x>0)的图象过点A(1,4),
∴m=1×4=4.
∵点B(4,n)在反比例函数y= ![]() 的图象上,
的图象上,
∴m=4n=4,解得:n=1.
∵在反比例函数y= ![]() (x>0)中,m=4>0,
(x>0)中,m=4>0,
∴反比例函数y= ![]() 的图象单调递减,
的图象单调递减,
∵0<x1<x2 ,
∴y1>y2 .
所以答案是:4;1;>.
【考点精析】认真审题,首先需要了解反比例函数的性质(性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大).

练习册系列答案
相关题目