题目内容
阅读理解:
对于任意正实数a,b,∵(
-
)2≥0,∴a-2
+b≥0,∴a+b≥2
,只有当a=b时,等号成立.若ab为定值P,则a+b≥2
,只有当a=b时,a+b有最小值2
.
(1)如图1,AB为半圆O的直径,C为半圆上的任意一点,(与点A、B不重合)过点C作CD⊥AB,垂足为D,AD=a,DB=b.根据图象验证,a+b≥2
,并指出等号成立时的条件.

(2)根据上述内容,回答下列问题
①若m>0,只有当m=
有最小值为
②如图2所示:A(-3,0),B(0,-4),P为双曲线y=
(x>0)上任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D,求四边形ABCD面积的最小值,并说明此时ABCD的形状.
对于任意正实数a,b,∵(
| a |
| b |
| ab |
| ab |
| P |
| P |
(1)如图1,AB为半圆O的直径,C为半圆上的任意一点,(与点A、B不重合)过点C作CD⊥AB,垂足为D,AD=a,DB=b.根据图象验证,a+b≥2
| ab |

(2)根据上述内容,回答下列问题
①若m>0,只有当m=
1
1
时,m+| 1 |
| m |
2
2
.②如图2所示:A(-3,0),B(0,-4),P为双曲线y=
| 12 |
| x |
分析:(1)先证明△ACD∽△CBD可得CD与
之间的关系,根据半径与a,b之间的等量关系,以及半径大于CD可得相关结论.
(2)①根据材料信息,可直接得出m的值,及m+
的最小值.
②设出的点P的坐标,根据对角线互相垂直的四边形的面积的求法,表示出四边形ABCD的面积,然后根据材料信息得出面积的最小值,也可判断出此时四边形ABCD的形状.
| ab |
(2)①根据材料信息,可直接得出m的值,及m+
| 1 |
| m |
②设出的点P的坐标,根据对角线互相垂直的四边形的面积的求法,表示出四边形ABCD的面积,然后根据材料信息得出面积的最小值,也可判断出此时四边形ABCD的形状.
解答:解:(1)AB是⊙O的直径,
 ∴AC⊥BC,
∴AC⊥BC,
又∵CD⊥AB,
∴∠CAD=90°-∠B=∠BCD,
∴Rt△CAD∽Rt△BCD,
∴CD2=AD•DB=ab,
∴CD=
,
若点D与O不重合,连OC,
在Rt△OCD中,OC>CD,则
>
,
若点D与O重合时,OC=CD,则
=
.
综上所述
≥
,即a+b≥2
,且当a=b时,等号成立.
(2)①由所给信息可得:m+
≥2
=2,且当m=
时,等号成立,
即可得若m>0,只有当m=1时,m+
有最小值为2.
②设P(x,
),则C(x,0),D(0,
),CA=x+3,DB=
+4,
则S四边形ABCD=
CA×DB=
(x+3)×(
+4),
化简得:S四边形ABCD=2(x+
+12),
∵x>0,
>0,
∴x+
≥2
=6,
只有当x=
即x=3时,等号成立.
则S≥2×6+12=24,
即当x=3时,S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,
故可得四边形ABCD是菱形.
 ∴AC⊥BC,
∴AC⊥BC,又∵CD⊥AB,
∴∠CAD=90°-∠B=∠BCD,
∴Rt△CAD∽Rt△BCD,
∴CD2=AD•DB=ab,
∴CD=
| ab |
若点D与O不重合,连OC,
在Rt△OCD中,OC>CD,则
| a+b |
| 2 |
| ab |
若点D与O重合时,OC=CD,则
| a+b |
| 2 |
| ab |
综上所述
| a+b |
| 2 |
| ab |
| ab |
(2)①由所给信息可得:m+
| 1 |
| m |
m×
|
| 1 |
| m |
即可得若m>0,只有当m=1时,m+
| 1 |
| m |
②设P(x,
| 12 |
| x |
| 12 |
| x |
| 12 |
| x |
则S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| x |
化简得:S四边形ABCD=2(x+
| 9 |
| x |
∵x>0,
| 9 |
| x |
∴x+
| 9 |
| x |
x•
|
只有当x=
| 9 |
| x |
则S≥2×6+12=24,
即当x=3时,S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,
故可得四边形ABCD是菱形.
点评:此题属于反比例函数综合题,注意仔细阅读材料,获取解题需要的信息,另外要注意对角线互相垂直的四边形的面积等于对角线乘积的一半,有一定难度.

练习册系列答案
相关题目
 问栏杆多少长时,所用拉力F最小?是多少?
问栏杆多少长时,所用拉力F最小?是多少?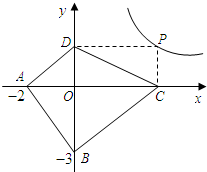 阅读理解:对于任意正实数a,b,
阅读理解:对于任意正实数a,b, 阅读理解:
阅读理解: