题目内容
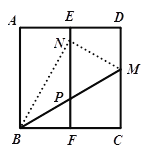
【题目】如图所示，用三种大小不同的5个正方形和一个长方形(阴影部分)拼成长方形ABCD，其中EF=2厘米，最小的正方形的边长为x厘米.
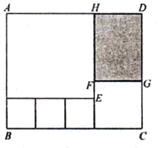
（1）用含x的代数式表示FG=________厘米，DG=________厘米.
（2）若长方形ABCD的周长等于52，求x的值
（3）若FG：DG=2：3，求四边形FGDH(阴影部分)的面积.
【答案】（1）(x＋2)；(3x－2)；（2）3；（3）
.
【解析】
（1）由图可知，
，GC等于最小正方形的边长与EF之和；因为最大正方形的边长是最小正方形边长的3倍，即为
，则
；
（2）由图可知，
，
，再利用长方形的周长公式列出等式，求解即可得；
（3）根据题（1）求出的用x表示的FG和DG，代入
化简计算得出x的值，从而得知FG和DG的值，最后利用长方形的面积公式即可得.
（1）由图可知，，GC等于最小正方形的边长与EF之和
则
由图可知，最大正方形的边长是最小正方形边长的3倍，即为
则；
（2）由图可知，，
则长方形ABCD的周长为: 
由题意得：
，解得：
；
（3）由题（1）知，
代入得：
解得：
则
故四边形FGDH的面积为
.
【题目】为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根调查结果绘制成的统计图（部分）如图所示．
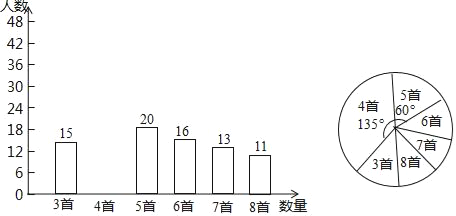
大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
（1）活动启动之初学生“一周诗词诵背数量”的中位数为 ；
（2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；
（3）选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．
