Question

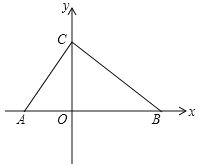
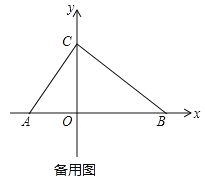
【题目】如图，在平面直角坐标系内，点 O 为坐标原点，点 A 在 x 轴负半轴上，点 B、C 分别在 x 轴、y 轴正半轴上，且 OB=2OA，OB﹣OC=OC﹣OA=2．

（1）求点 C 的坐标；

（2）点 P 从点 A 出发以每秒 1 个单位的速度沿 AB 向点 B 匀速运动，同时点 Q 从点 B 出发 以每秒 3 个单位的速度沿 BA 向终点 A 匀速运动，当点 Q 到达终点 A 时，点 P、Q 均停止运 动，设点 P 运动的时间为 t 秒（t＞0），线段 PQ 的长度为 y，用含 t 的式子表示 y，并写出 相应的 t 的范围；

（3）在（2）的条件下，过点 P 作 x 轴的垂线 PM，PM=PQ，是否存在 t 值使点 O 为 PQ 中 点？若存在求 t 值并求出此时三角形 CMQ 的面积；若不存在，请说明理由．

Answer 1

【答案】（1）点 C 的坐标为（0，6）；（2）y=12﹣4t（0＜t≤3），y=4t﹣12（3＜t≤4）；（3）存在 t 值使点 O 为 PQ 中点，三角形 CMQ 的面积为：8 或 16．

【解析】分析：（1）设A（x，0），则OA=-x，OB=-2x，OC=-2x-2，进而可得B（-2x，0），C（0，-2x-2），然后根据OC-OA=2，可得x=-4，进而可得点C的坐标；
（2）由（1）可知AB=OA+OB=12，由点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动，当点Q到达终点A时，点P、Q均停止运动，可得t的最大值为4秒，然后求出P、Q两点相遇时的t的值为：12÷（1+3）=3秒，然后分两种情况讨论即可：①0＜t≤3；②3＜t≤4；
（3）点O为PQ中点，可知0＜t≤3，OP=OQ，即OA-AP=OB-BP，进而可求t的值；然后分两种情况讨论即可：①点M在x轴上方；②点M在x轴下方．

详解：（1）∵点A在x轴负半轴上，点B、C分别在x轴、y轴正半轴上，OB=2OA，

OB﹣OC=OC﹣OA=2．设A（x，0），

∴OA=﹣x，OB=﹣2x，OC=﹣2x﹣2，

∴B（﹣2x，0），C（0，﹣2x﹣2），

∵OC﹣OA=2，

∴﹣2x﹣2﹣（﹣x）=2，解得：x=﹣4，

∴OA=4，OB=8，OC=6，点A的坐标为（﹣4，0），点B的坐标为（8，0），点C的坐标为（0，6）；

（2）由（1）知：AB=OA+OB=12，

∵点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动，同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动，

∴点P运动的时间为t（t＞0）秒时，AP=t，BQ=3t，当P、Q两点相遇时的t的值为：12÷（1+3）=3秒，

∵当点Q到达终点A时，点P、Q均停止运动，

∴t的最大值为12÷3=4秒.

①当0＜t≤3时，如图1，

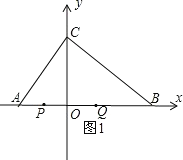
PQ=AB﹣AP﹣QB=12﹣t﹣3t=12﹣4t，

即y=12﹣4t（0＜t≤3）；

②当3＜t≤4时，如图2，

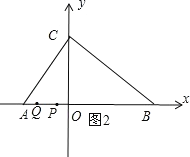
PQ=AP+BQ-AB=4t-12,即y=4t-12().

（3）存在t值使点O为PQ中点，

∵点O为PQ中点，

∴0＜t≤3，OP=OQ，即OA﹣AP=OB﹣BQ，

∴4-t=8-3t,

当t=2时，AP=2，OP=2，OQ=2，PQ=4，PM=PQ=4，

①点M在x轴上方时，如图3，

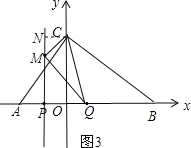
过点C作CN⊥PM，得：四边形CNPQ是梯形，

∵S△CMQ=S梯形CNPQ﹣S△CNM﹣S△PQM，

∴S△CMQ=（CN+PQ）×PN﹣CNMN﹣PMPQ，

=（OP+PQ）×OC﹣×OP×（OC﹣PM）﹣×4×4，

=（2+4）×6﹣2×（6﹣4）﹣8，

=18﹣2﹣8，

=8；

②点M在x轴下方，如图4．

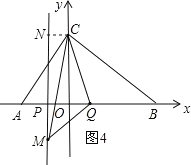
过点C作CN⊥PM，得：四边形CNPQ是梯形，

∵S△CMQ=S梯形CNPQ+S△PQM﹣S△CNM，

∴S△CMQ=（CN+PQ）PN+PQPM﹣MNCN，

=（OP+PQ）×OC+×4×4﹣（OC+PM）OP，

=（2+4）×6+8﹣（6+4）×2，

=+8﹣，

=18+8﹣10，

=16．

∴三角形CMQ的面积为：8或16．