题目内容
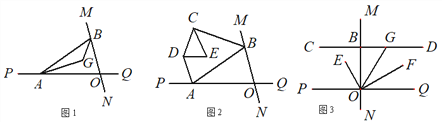
【题目】如图，在Rt△ACB中，∠C=90°，BE平分∠ABC，ED垂直平分AB于D，则图中的全等三角形对数共有（ ）
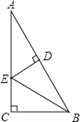
A. 1对 B. 2对 C. 3对 D. 4对
【答案】C
【解析】分析：由在Rt△ACB中，∠C=90°，BE平分∠ABC，ED垂直平分AB，利用HL易证得Rt△EBC≌Rt△EBD与Rt△EAD≌Rt△EBD，继而可得△AED≌△BCE．
详解：∵ED垂直平分AB，
∴AE=BE，ED⊥AB，
∵在Rt△ACB中,∠C=90°，BE平分∠ABC，
∴EC=ED，
在Rt△ECB和Rt△EDB中，
EC=ED，BE=BE，
∴Rt△EBC≌Rt△EBD(HL)，
在Rt△EAD和Rt△EBD中，
AE=BE，DE=DE，
∴Rt△EAD≌Rt△EBD(HL)，
∴△AED≌△BCE.
∴图中的全等三角形对数共有3对.
故选C.
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
【题目】某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：
A | B | |
进价（万元/套） | 1.5 | 1.2 |
售价（万元/套） | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元。
（毛利润=（售价 - 进价）×销售量）
（1）该商场计划购进A，B两种品牌的教学设备各多少套？
（2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？
【题目】某剧院的观众席的座位为扇形，且按下列分式设置：
排数（x） | 1 | 2 | 3 | 4 | … |
座位数（y） | 50 | 53 | 56 | 59 | … |
（1）按照上表所示的规律，当x每增加1时，y如何变化？
（2）写出座位数y与排数x之间的关系式；
（3）按照上表所示的规律，某一排可能有90个座位吗？说说你的理由．
