题目内容
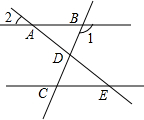 如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的
如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的
- A.BC=AE
- B.CD2+DE2=CE2
- C.CE=2CD
- D.BC⊥AE
A
分析:根据对顶角相等可求出∠ADB为直角,根据直角三角形中30°角直角边等于斜边的一半,结合各选项的说法即可作出判断.
解答:∵∠1=120°,∠2=30°,
∴∠ABD=60°,∠BAD=30°,
∴∠ADB=∠CDE=90°.
A、本题没有涉及线段的相等,不能确定BC=AE,故本选项错误;
B、在RT△CDE中利用勾股定理即可得出CD2+DE2=CE2,故本选项正确;
C、在RT△CDE中,∠CED=∠BAD=30°,即可得出CE=2CD,故本选项正确;
D、∠ADB=∠CDE=90°,即可得出BC⊥AE,故本选项正确;
故选A.
点评:本题考查了勾股定理、平行四边形的性质及含30°角的直角三角形,判断出BC⊥AE是解答本题的关键,另外要熟悉掌握勾股定理的表达式及直角三角形中30°角直角边等于斜边的一半.
分析:根据对顶角相等可求出∠ADB为直角,根据直角三角形中30°角直角边等于斜边的一半,结合各选项的说法即可作出判断.
解答:∵∠1=120°,∠2=30°,
∴∠ABD=60°,∠BAD=30°,
∴∠ADB=∠CDE=90°.
A、本题没有涉及线段的相等,不能确定BC=AE,故本选项错误;
B、在RT△CDE中利用勾股定理即可得出CD2+DE2=CE2,故本选项正确;
C、在RT△CDE中,∠CED=∠BAD=30°,即可得出CE=2CD,故本选项正确;
D、∠ADB=∠CDE=90°,即可得出BC⊥AE,故本选项正确;
故选A.
点评:本题考查了勾股定理、平行四边形的性质及含30°角的直角三角形,判断出BC⊥AE是解答本题的关键,另外要熟悉掌握勾股定理的表达式及直角三角形中30°角直角边等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 8、如图,已知AB∥CE,∠C=30°,BC平分∠ABD,则∠BDC=
8、如图,已知AB∥CE,∠C=30°,BC平分∠ABD,则∠BDC= 如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的( )
如图,已知AB∥CE,AE与BC交于点D,∠1=120°,∠2=30°,则下列说法不正确的( )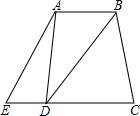 如图,已知AB∥CE,DB平分∠ADC,AE∥BD,∠C=2∠E,求证:四边形ABCD是等腰梯形.
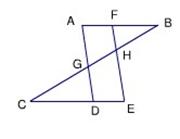
如图,已知AB∥CE,DB平分∠ADC,AE∥BD,∠C=2∠E,求证:四边形ABCD是等腰梯形.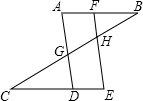 如图,已知AB∥CE,∠A=∠E,试说明:∠CGD=∠FHB.
如图,已知AB∥CE,∠A=∠E,试说明:∠CGD=∠FHB.