题目内容
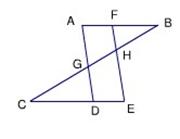
8、如图，已知AB∥CE，∠C=30°，BC平分∠ABD，则∠BDC=120
度．分析：由AB∥CE，∠C=30°，根据两直线平行，内错角相等，即可求得∠ABC的度数，又由BC平分∠ABD，求得∠ABD的度数，然后根据两直线平行，同旁内角互补，即可求得∠BDC的度数．
解答：解：∵AB∥CE，∠C=30°，
∴∠ABC=∠C=30°，
∵BC平分∠ABD，
∴∠ABD=2∠ABC=60°，
∵AB∥CE，
∴∠BDC+∠ABD=180°，
∴∠BDC=120°．
故答案为120．
∴∠ABC=∠C=30°，
∵BC平分∠ABD，
∴∠ABD=2∠ABC=60°，
∵AB∥CE，
∴∠BDC+∠ABD=180°，
∴∠BDC=120°．
故答案为120．
点评：此题考查了平行线的性质．注意掌握两直线平行，同旁内角互补与两直线平行，内错角相等定理的应用是解此题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
如图，已知AB∥CE，AE与BC交于点D，∠1=120°，∠2=30°，则下列说法不正确的（ ）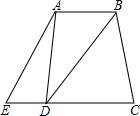
如图，已知AB∥CE，DB平分∠ADC，AE∥BD，∠C=2∠E，求证：四边形ABCD是等腰梯形．
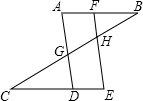如图，已知AB∥CE，∠A=∠E，试说明：∠CGD=∠FHB．