题目内容
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 | 空调 | 彩电 | 冰箱 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)
【答案】解:设每周应生产空调、彩电、冰箱的数量分别为x台、y台、z台,则有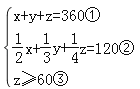 ,
,
①﹣②×4得3x+y=360,
总产值A=4x+3y+2z=2(x+y+z)+(2x+y)=720+(3x+y)﹣x=1080﹣x,
∵z≥60,
∴x+y≤300,
而3x+y=360,
∴x+360﹣3x≤300,
∴x≥30,
∴A≤1050,
即x=30,y=270,z=60.
最高产值:30×4+270×3+60×2=1050(千元)
【解析】设每周应生产空调、彩电、冰箱的数量分别为x台、y台、z台,建立三元一次方程组,则总产值A=4x+3y+2z,由于每周冰箱至少生产60台,即z≥60,所以x+y≤300,又由于生产空调器、彩电、冰箱共360台,故有x≥30台,即可求得,具体的x,y,z的值.
【考点精析】通过灵活运用解三元一次方程组,掌握通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程即可以解答此题.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】森林公园的门票价格规定如下表:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 13元 | 11元 | 9元 |
某校初一(5)(6)两个班共104人去游森林公园,其中(5)班人数较少,不到50人;(6)班人数较多,(6)班人数多于50人且少于100人.经估算,如果两班都是以班为单位分别购票则一共应付1240元;
(1)求这两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?