题目内容
【题目】如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.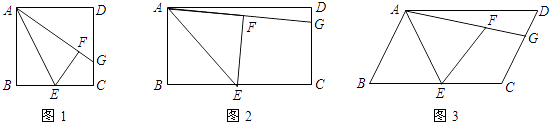
(1)猜想并证明线段GF与GC的数量关系;
(2)若将图1中的正方形改成矩形,其它条件不变,如图2,那么线段GF与GC之间的数量关系是否改变?请证明你的结论;
(3)若将图1中的正方形改成平行四边形,其它条件不变,如图3,那么线段GF与GC之间的数量关系是否会改变?请证明你的结论.
【答案】
(1)
解:FG=CG,理由如下:
∵E是BC的中点
∴BE=CE
∵将△ABE沿AE折叠后得到△AFE
∴BE=EF,
∴EF=EC;
同样,在折叠中,∠B=∠EFA=90°
又∵∠C=∠B,∠EFG=∠EFA
∴∠C=∠EFG=90°
∵EG=EG,
∴△ECG≌△EFG
∴FG=CG
(2)
解:不会改变.
证明:连接EG
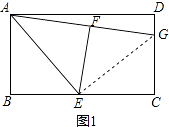
∵E是BC的中点
∴BE=CE
∵将△ABE沿AE折叠后得到△AFE
∴BE=EF,
∴EF=EC;
同样,在折叠中,∠B=∠EFA=90°
又∵∠C=∠B,∠EFG=∠EFA
∴∠C=∠EFG=90°
∵EG=EG,
∴△ECG≌△EFG
∴FG=CG;
(3)
解:不会改变.
证明:连接EG、FC
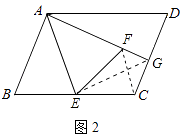
∵E是BC的中点
∴BE=CE
∵将△ABE沿AE折叠后得到△AFE
∴BE=EF,∠B=∠AFE
∴EF=EC
∴∠EFC=∠ECF
∵矩形ABCD改为平行四边形
∴∠B=∠D
∵∠ECD=180°﹣∠D,∠EFG=180°﹣∠AFE=180°﹣∠B=180°﹣∠D
∴∠ECD=∠EFG
∴∠GFC=∠GFE﹣∠EFC=∠ECG﹣∠ECF=∠GCF
∴∠GFC=∠GCF
∴△ECG≌△EFG
∴FG=CG
即(1)中的结论仍然成立
【解析】(1)判定直角三角形△ECG和△EFG全等,和全等三角形对应边相等的性质;(2)判定直角三角形△ECG和△EFG全等,和全等三角形对应边相等的性质;(3)判定△ECG和△EFG全等,根据全等三角形对应边相等性质即可证明.