题目内容
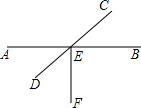
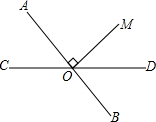
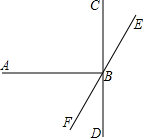
如图，AB⊥CD，垂足为B，EF是经过B点的一条直线，已知∠EBD=145°，则∠CBE，∠ABF的度数分别为（ ）
| A．55°，35° | B．35°，55° | C．45°，45° | D．25°，55° |
∵∠CBE+∠EBD=180°，∠EBD=145°，
∴∠CBE=180°-∠EBD=35°，
∵∠CBE与∠DBF是对顶角，
∴∠DBF=∠CBE=35°，
∵AB⊥CD，
∴∠ABF=90°-∠DBF=55°．
故选B．
∴∠CBE=180°-∠EBD=35°，
∵∠CBE与∠DBF是对顶角，
∴∠DBF=∠CBE=35°，
∵AB⊥CD，
∴∠ABF=90°-∠DBF=55°．
故选B．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
