题目内容
【题目】如图,在等腰三角形ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线相交于点O,点C沿EF折叠后与点O重合,求∠CEF的度数.

【答案】50°
【解析】试题分析:连接OB,根据中垂线的性质就可以得出AO=BO,就有∠OAB=∠OBA,根据角平分线的性质就可以求出∠EBO的度数,通过△ABO≌△ACO就有BO=CO,就有∠OBC=∠OCB,再由轴对称就可以求出OE=CE,从而求出结论.
试题解析:连接OB,
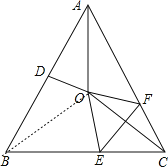
∵OD垂直平分AB,
∴AO=BO,
∴∠OAB=∠OBA.
∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°.
∵OA平分∠BAC,
∴∠BAO=∠CAO=![]() ∠BAC=25°,
∠BAC=25°,
∴∠OBA=25°,
∴∠OBC=40°.
在△ABO和△ACO中
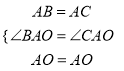 ,
,
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=40°.
∵△EOF与△ECF关于EF对称,
∴△EOF≌△ECF,
∴OE=CE,∠OEF=∠CEF=![]() ∠OEC..
∠OEC..
∴∠ECO=∠EOC=40°,
∴∠OEC=100°,
∴∠CEF=50°.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m﹣3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
