题目内容
4. 如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求tan∠EBC的值.
如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求tan∠EBC的值.
分析 由矩形的性质得出AD=BC,AD∥BC,∠A=90°,由勾股定理得出AE,由平行线的性质得出∠AEB=∠EBC,再由三角函数的定义即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠A=90°,
又∵BE=AD,BC=10,
∴BE=10,
∵∠A=90°
∴AB2+AE2=BE2,
∴AE=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵AD∥BC,
∴∠AEB=∠EBC,
∴tan∠EBC=tan∠AEB=$\frac{AB}{AE}$=$\frac{6}{8}$=$\frac{3}{4}$.
点评 本题考查了矩形的性质、勾股定理、平行线的性质、三角函数;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
14.下面计算正确的是( )
| A. | 3a-2a=1 | B. | 3a2+2a=5a3 | C. | 3a+3b=6ab | D. | 2x+3x=5x |
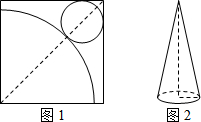 如图,在纸上剪下一个扇形和一个圆形,使之恰好围成一个圆锥,若圆的半径为1cm,若扇形的圆心角等于90°,则扇形的半径为4cm.
如图,在纸上剪下一个扇形和一个圆形,使之恰好围成一个圆锥,若圆的半径为1cm,若扇形的圆心角等于90°,则扇形的半径为4cm.
 如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长和菱形的面积.
如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长和菱形的面积. 如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE=30°.
如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE=30°.