题目内容
19.已知甲数的绝对值是乙数绝对值的2倍,两数在数轴上对应两点之间的距离为6,这两数的积为72,±8.分析 根据绝对值的定义和正负数的意义,利用分类讨论的思想:同在原点的右侧,设乙为x,则甲为2x,由题意可得2x-x=6,可得甲数和乙数;若同在原点的左侧,设乙为x,则甲为2x,x-2x=6,可得甲数和乙数;在原点的两侧,设乙为x,则甲为-2x,由题意可得x+2x=6,可得甲数和乙数;若原点的两侧,设乙为-x,则甲为2x,-x+2x=6,可得甲数和乙数.再写出即可求解.
解答 解:①同在原点的右侧,设乙为x,则甲为2x,由题意可得
2x-x=6,
解得x=6,
2x=12,
xy=6×12=72;
②若同在原点的左侧,设乙为x,则甲为2x,由题意可得
x-2x=6,
解得x=-6,
-2x=-12,
xy=(-6)×(-12)=72;
③在原点的两侧,设乙为x,则甲为-2x,由题意可得
x+2x=6,
解得x=2,
-2x=-4,
xy=2×(-4)=8;
④若原点的两侧,设乙为-x,则甲为2x,由题意可得
-x-2x=6,
解得x=-2,
-2x=4,
xy=-2×4=-8;
故这两数的积为72,±8.
故答案为:72,±8.
点评 本题主要考查了绝对值的定义和正负数的意义,根据题意列出方程是解答此题的关键.

练习册系列答案
相关题目
7.估计$\sqrt{41}$介于( )
| A. | 5与6之间 | B. | 6与7之间 | C. | 7与8之间 | D. | 8与9之间 |
9.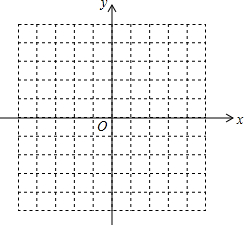 已知二次函数y=x2+4x.
已知二次函数y=x2+4x.
(1)用配方法把它变成y=a(x-h)2+k的形式,
(2)在给定的平面直角坐标系中,画出这个函数的图象;
(3)若将此图象沿x轴向右平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式y=x2-2x-4.
 已知二次函数y=x2+4x.
已知二次函数y=x2+4x.(1)用配方法把它变成y=a(x-h)2+k的形式,
(2)在给定的平面直角坐标系中,画出这个函数的图象;
| x | … | -5 | -4 | -2 | 0 | 1 | … |
| y | … | 5 | 0 | -4 | 0 | 5 | … |
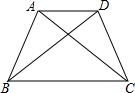 如图,已知∠CBD=∠ACB,要说明△ABC≌△DCB,
如图,已知∠CBD=∠ACB,要说明△ABC≌△DCB, 如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求tan∠EBC的值.
如图,点E是矩形ABCD的边AD上一点,且BE=AD,如果AB=6,BC=10,求tan∠EBC的值.