题目内容
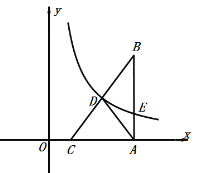
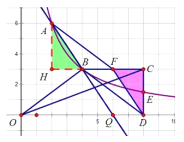
【题目】如图①,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,![]() 轴(点
轴(点![]() 在点
在点![]() 的右侧),且
的右侧),且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() .
.
(1)求![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)填空:不等式![]() 的解集为______;
的解集为______;
(3)当![]() 平分
平分![]() 时,求
时,求![]() 的值;
的值;
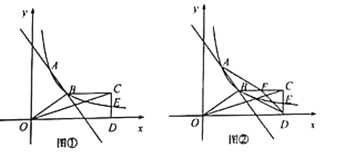
(4)如图②,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,当四边形
,当四边形![]() 为平行四边形时,求点
为平行四边形时,求点![]() 的坐标.
的坐标.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
【解析】
(1) 将![]() 代入
代入![]() 可求出b的值,将
可求出b的值,将![]() 代入
代入![]() ,可求得反比例函数的表达式;
,可求得反比例函数的表达式;
(2)在第一象限内,根据A、B坐标写出一次函数图象在反比例函数图象上上方所对应的自变量的范围即可;
(3)求出B点坐标,得出![]() 及
及![]() ,由
,由 ![]() 平分
平分![]() ,可得
,可得![]() ,由
,由![]() 轴,可推
轴,可推![]() ,可得
,可得![]() =5,可得
=5,可得![]() ,及
,及 ![]() ,
,![]() .可得
.可得![]() ,
,![]() ,代入
,代入![]() 即可.
即可.
(4)作![]() 交于点
交于点![]() ,则
,则![]() ,可得
,可得![]() ,
,![]() ,由平行四边形的性质可得
,由平行四边形的性质可得![]() ,
,![]() ,故
,故![]() ,可证
,可证![]() ,得到
,得到![]() ,由于
,由于![]() 为
为![]() 中点,故
中点,故![]() ,可得
,可得![]() .
.
(1)将![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴反比例函数的表达式为![]() .
.
(2)当y=3时![]() ,解得:x=4
,解得:x=4
∴B(4,3)
由图像可知不等式![]() 的解集为
的解集为![]() .
.
故答案为:![]()
(3)将![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
(4)作![]() 交于点
交于点![]() ,则
,则![]() .
.
∴![]() ,
,![]() ,
,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目