Question

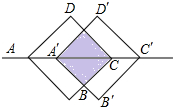如图，把正方形ABCD沿对角线AC的方向移动到正方形A′B′C′D′的位置，它们的重叠部分（图中的阴影部分）的面积是正方形ABCD面积的一半，若AD=2，则正方形移动的距离AA′的长是

 

．

Answer 1

分析：由图可知AA′=AC-A′C，其中AC是正方形ABCD的对角线，根据勾股定理可知AC=

2

AD=2

2

，关键是求A′C的长度．由平移的性质可知它们的重叠部分是一个正方形，又知其面积是正方形ABCD面积的一半，从而求出A′C的长度，进而得出结果．

解答：解：把正方形ABCD沿对角线AC的方向移动到正方形A′B′C′D′的位置，则它们的重叠部分是一个正方形．
又∵它们的重叠部分的面积是正方形ABCD面积的一半，
∴它们的重叠部分的面积=

1

2

×2×2=2，
∴A′C=2．
又∵AC是正方形ABCD的对角线，
∴AC=

2

AD=2

2

，
∴AA′=AC-A′C=2

2

-2．
故答案为2

2

-2．

点评：本题结合图形的平移考查了正方形的性质及勾股定理等知识．平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．