题目内容
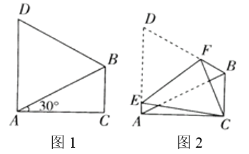
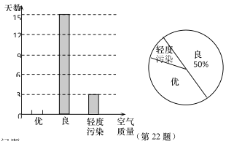
【题目】如图,四边形![]() 中,
中, ![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
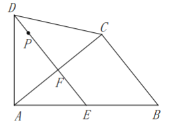
(1)求证:![]() 是
是![]() 的中点.
的中点.
(2)已知![]() ,
,![]() 是射线
是射线![]() 上的动点.设
上的动点.设![]() ,
,
①若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关
关![]() 于的函数关系式;
于的函数关系式;
②在①中,当![]() 为何值时,
为何值时,![]() 的周长最小,并求出此时
的周长最小,并求出此时![]() 的值.
的值.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)根据平行线的性质求出![]() ,根据
,根据![]() ,推出
,推出![]() ,即可得出答案;
,即可得出答案;
(2)①根据勾股定理求出AC,求出CF的长,得出四边形BCDP是梯形,根据梯形的面积公式得出即可;
②求出CP+BP最小时,△BCP的周长最小,根据对称得出当P到E时,△PBC的周长最小,证△DAE∽△ACB,得出比例式,求出DE的值即可.
(1)证明:![]()
![]()
![]()
![]()
![]() ,即
,即![]() 是
是![]() 的中点
的中点
(2)①在Rt△ACB中,AB=15,BC=9,由勾股定理得:
![]()
∵DF∥BC,
∴梯形BCDP的面积y=![]() (x+9)×6=3x+27,
(x+9)×6=3x+27,
即y=3x+27(x>0).
②△PBC的周长是BC+CP+PB=9cm+CP+BP,
要使△PBC的周长最小,只要CP+BP最小即可,
∵CF=AF,DE⊥AC,
∴C、A关于DF对称,
即当点P运动到点E时,CP+BP最小,此时△PBC的周长最小, 求得AE=BE=![]() AB=
AB=![]() cm,
cm,
∵DE∥BC,
∴∠DEA=∠CBA,
∵∠DAE=∠ACB=90°,
∴△DAE∽△ACB,
∴![]() ,
,
∴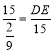 ,
,
![]()
![]() 当
当![]() 时,
时,![]() 的周长最小,此时
的周长最小,此时![]() .
.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
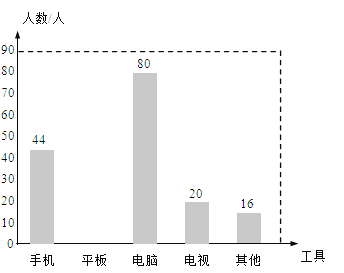
名校名卷单元同步训练测试题系列答案【题目】在“停课不停学”期间,某校数学兴趣小组对本校同学观看教学视频所使用的工具进行了调查,并从中随机抽取部分数据进行分析,将分析结果绘制成了两幅不完整的统计表与统计图.
工具 | 人数 | 频率 |
手机 | 44 | a |
平板 | b | 0.2 |
电脑 | 80 | c |
电视 | 20 | d |
不确定 | 16 | 0.08 |
请根据上述信息回答下列问题:
(1)所抽取出来的同学共 人,表中a= ,b= ;
(2)请补全条形统计图;
(3)若该校观看教学视频的学生总人数为2500人,则使用电脑的学生人数约 人.![]()
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题:
(1)m= ,n= ,p= ;
(2)请根据以上信息直接补全条形统计图;

(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.