题目内容
【题目】如图, ![]() 是半径为
是半径为 ![]() 的⊙
的⊙ ![]() 的直径,
的直径, ![]() 是圆上异于
是圆上异于 ![]() ,
, ![]() 的任意一点,
的任意一点, ![]() 的平分线交⊙
的平分线交⊙ ![]() 于点
于点 ![]() ,连接
,连接 ![]() 和
和 ![]() ,△
,△ ![]() 的中位线所在的直线与⊙
的中位线所在的直线与⊙ ![]() 相交于点
相交于点 ![]() 、
、 ![]() ,则
,则 ![]() 的长是.
的长是.
【答案】4 ![]()
【解析】如图所示:
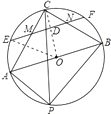
∵PC是∠APB的角平分线,∴∠APC=∠CPB,
![]()
![]() ∴AC=BC
∴AC=BC
∵AB是直径,
∴∠ACB=90.
即△ABC是等腰直角三角形,
连接OC,交EF于点D,则OC⊥AB;
∵MN是△ABC的中位线,
∴MN∥AB;
∴OC⊥EF,OD= ![]() OC=2.
OC=2.
连接OE,根据勾股定理,得:DE= ![]() =2
=2 ![]() ,
,
∴EF=2ED=4 ![]() .
.
故答案为:![]() .
.
连接OE、OC,交EF于点D.易证出△ABC是等腰直角三角形,则OC⊥AB;由MN是△ABC的中位线可知OC⊥EF,进而求出OD的长,再由勾股定理可求出DE的长,由垂径定理可得EF的长.

练习册系列答案
相关题目









