题目内容
【题目】已知△ABC,∠ACB=90°,点D(0,-3),M(4,-3).
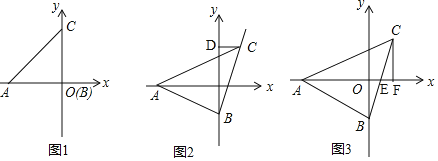
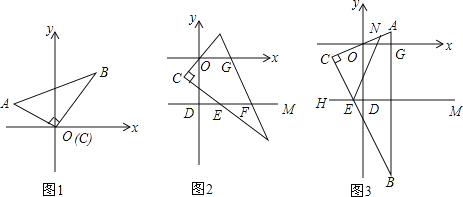
(1)如图1,若点C与点O重合,且A(-3,a),B(3,b),a+b-8=0,求△ACB的面积;
(2)如图2,若∠AOG=50°,求∠CEF的度数;
(3)如图3,旋转△ABC,使∠C的顶点C在直线DM与x轴之间,N为AC上一点,E为BC与DM的交点∠NEC+∠CEF=180°,下列两个结论:
①∠NEF-∠AOG为定值;②![]() 为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
【答案】(1)△ACB的面积为12;(2)∠CEF的度数为140°;(3)![]() 为定值,其值为3.
为定值,其值为3.
【解析】试题分析:(1)过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,根据![]() 的面积等于梯形
的面积等于梯形![]() 的面积减去两个直角三角形的面积列式计算即可得解;
的面积减去两个直角三角形的面积列式计算即可得解;
(2)根据对顶角相等和互余的性质得出![]() 再根据邻补角得出
再根据邻补角得出![]() 即可;
即可;
(3)作![]() 轴,则
轴,则![]() 轴,根据平行线的性质得
轴,根据平行线的性质得![]() 由于
由于![]() 所以
所以![]() 然后利用
然后利用![]() 即可得到
即可得到![]()
试题解析:(1)如图1,过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,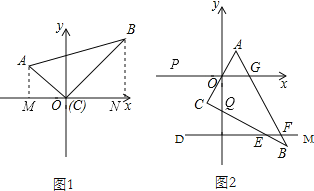
∵A(3,a),B(3,b),
∴AM=a,OM=3,BN=b,ON=3,
∴MN=3+3=6,
△ABC的面积![]()
∵a+b8=0,
∴a+b=8
∴△ABC的面积![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 为定值.理由如下:
为定值.理由如下:
作![]() 轴,如图3,
轴,如图3,
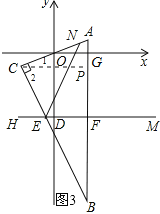
则![]() 轴,
轴,
![]()
而![]()
![]()
![]()
![]()
![]()
![]()
∴可得: ![]()
可得![]() 是定值.
是定值.

练习册系列答案
相关题目