题目内容
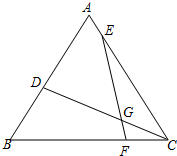如图，等边△ABC中，D、E、F分别是AB、AC、BC上的点，连接CD、EF交于点G，且∠CGF=60°．（1）请直接写出图中所有与△BDC相似的三角形（不用证明）；
（2）若
| EF |
| DC |
| 4 |
| 5 |
| AE |
| EC |
分析：（1）根据等边三角形的性质及∠CGF=60°，可以得出∠B=∠ACB=∠CGF=60°，可以得出△BDC∽△GFC∽△CFE；
（2）由（1）△BDC∽△CFE可以得出
=
，再根据条件
=
和三角形ABC是等边三角形和线段的转化，就可以得出
的值．
（2）由（1）△BDC∽△CFE可以得出
| EF |
| DC |
| CE |
| BC |
| EF |
| DC |
| 4 |
| 5 |
| AE |
| EC |
解答：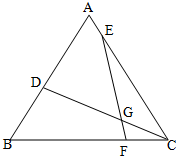
解：（1）△BDC相似的三角形：△GFC、△CFE；
（2）∵△BDC∽△CFE，
∴
=
．
∵
=
，
∴
=
．
∵等边△ABC，
∴AC=BC，
∴
=
，
即
=
．
解：（1）△BDC相似的三角形：△GFC、△CFE；（2）∵△BDC∽△CFE，
∴
| EF |
| DC |
| CE |
| BC |
∵
| EF |
| DC |
| 4 |
| 5 |
∴
| CE |
| CB |
| 4 |
| 5 |
∵等边△ABC，
∴AC=BC，
∴
| CE |
| AC |
| 4 |
| 5 |
即
| AE |
| EC |
| 1 |
| 4 |
点评：本题考查了相似三角形的判定与性质，等边三角形的性质．
练习册系列答案
相关题目
如图，等边△ABC中，AD是∠BAC的角平分线，E为AD上一点，以BE为一边且在BE下方作等边△BEF，连接CF．
如图，等边△ABC中，D、E、F分别是各边上的一点，且AD=BE=CF．
如图，等边△ABC中，D是BC上一点，以AD为边作等腰△ADE，使AD=AE，∠DAE=80°，DE交AC于点F，∠BAD=15°，求∠FDC的度数．
如图，等边△ABC中，AD=CE，BD和AE相交于F，BG⊥AE垂足为G，求∠FBG的度数．