题目内容
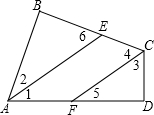
 17、如图,AE为∠BAD的平分线,CF为∠BCD的平分线,且AE∥CF,则∠B与∠D的关系为
17、如图,AE为∠BAD的平分线,CF为∠BCD的平分线,且AE∥CF,则∠B与∠D的关系为∠B=∠D
.分析:由AE∥CF,根据两直线平行,同位角相等,即可证得∠EAF=∠CFD,∠FCE=∠AEB,又由AE为∠BAD的平分线,CF为∠BCD的平分线与三角形内角和定理,易证得:∠B=∠D.
解答:解:∵AE∥CF,
∴∠EAF=∠CFD,∠FCE=∠AEB,
∵AE为∠BAD的平分线,CF为∠BCD的平分线,
∴∠BAE=∠EAD,∠DCF=∠FCE,
∴∠CFD=∠BAE,∠DCF=∠AEB,
∵∠B+∠BAE+∠BEA=180°,∠D+∠DFC+∠DCF=180°,
∴∠B=∠D.
故答案为:∠B=∠D.
∴∠EAF=∠CFD,∠FCE=∠AEB,
∵AE为∠BAD的平分线,CF为∠BCD的平分线,
∴∠BAE=∠EAD,∠DCF=∠FCE,
∴∠CFD=∠BAE,∠DCF=∠AEB,
∵∠B+∠BAE+∠BEA=180°,∠D+∠DFC+∠DCF=180°,
∴∠B=∠D.
故答案为:∠B=∠D.
点评:此题考查了平行线的性质,角平分线的定义以及三角形内角和定理.此题比较简单,解题的关键是注意掌握两直线平行,同位角相等定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
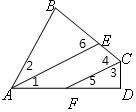 24、如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.
24、如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.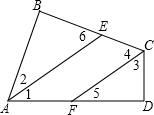 如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.
如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.