题目内容
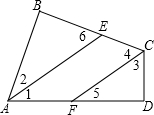
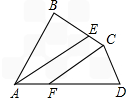
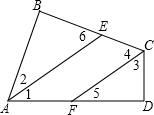 如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.
如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.
证明:如图,设:∠AEB=∠6,∠FCB=∠4,∠EAF=∠1,∠CFD=∠5,∠FCD=∠3,∠BAE=∠2.
∵AE∥CF(已知),
∴∠1=∠5,∠4=∠6(两直线平行,同位角相等),
∵AE平分∠BAD,CF平分∠BCD(已知),
∴∠1=∠2,∠3=∠4(角平分线性质),
∴∠2=∠5,∠3=∠6(等量代换),
∵∠2+∠6+∠B=180°,∠3+∠5+∠D=180°(三角形内角和定理),
∴∠B=∠D(等量代换).
分析:从AE∥CF,可以得到:∠AEB=∠FCB,∠EAF=∠CFD,再从两个角平分线和三角形内角和定理来解答.
点评:该题通过观察,分析并找到联系,建立关系式从而证明结果.
∵AE∥CF(已知),
∴∠1=∠5,∠4=∠6(两直线平行,同位角相等),
∵AE平分∠BAD,CF平分∠BCD(已知),
∴∠1=∠2,∠3=∠4(角平分线性质),
∴∠2=∠5,∠3=∠6(等量代换),
∵∠2+∠6+∠B=180°,∠3+∠5+∠D=180°(三角形内角和定理),
∴∠B=∠D(等量代换).
分析:从AE∥CF,可以得到:∠AEB=∠FCB,∠EAF=∠CFD,再从两个角平分线和三角形内角和定理来解答.
点评:该题通过观察,分析并找到联系,建立关系式从而证明结果.

练习册系列答案
相关题目
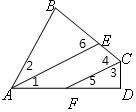 24、如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D.
24、如图,AE为∠BAD的角平分线,CF为∠BCD的角平分线,且AE∥CF,求证:∠B=∠D. 17、如图,AE为∠BAD的平分线,CF为∠BCD的平分线,且AE∥CF,则∠B与∠D的关系为
17、如图,AE为∠BAD的平分线,CF为∠BCD的平分线,且AE∥CF,则∠B与∠D的关系为