题目内容
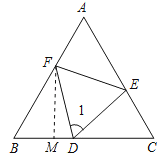
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在边BC,AC,AB上,且BD=CE,DC=BF,连结DE,EF,DF,∠1=60°
(1)求证:△BDF≌△CED.
(2)判断△ABC的形状,并说明理由.
(3)若BC=10,当BD= 时,DF⊥BC.(只需写出答案,不需写出过程)

【答案】(1)见解析;(2)△ABC是等边三角形,见解析;(3)![]()
【解析】
(1)由等腰三角形的性质得出∠B=∠C,由已知条件即可得出△BDF≌△CED(SAS);
(2)由(1)得△BDF≌△CED,得出∠BFD=∠CDE,证出∠B=∠1=60°,即可得出△ABC是等边三角形;
(3)作FM⊥BC于M,由(1)得△BDF≌△CED,得出BF=CD,由(2)得△ABC是等边三角形,得出∠B=∠C=60°,证出∠BFM=30°,得出BM=![]() BF=
BF=![]() CD,BM=
CD,BM=![]() BC=
BC=![]() ,得出M与D重合,即可得出结论.
,得出M与D重合,即可得出结论.
(1)∵AB=AC,
∴∠B=∠C,
在△BDF和△CED中, ,
,
∴△BDF≌△CED(SAS);
(2)△ABC是等边三角形,理由如下:
由(1)得:△BDF≌△CED,
∴∠BFD=∠CDE,
∵∠CDF=∠B+∠BFD=∠1+∠CDE,
∴∠B=∠1=60°,
∵AB=AC,
∴△ABC是等边三角形;
(3)当BD=![]() 时,DF⊥BC,理由如下:
时,DF⊥BC,理由如下:
作FM⊥BC于M,如图所示:
由(1)得:△BDF≌△CED,
∴BF=CD,
由(2)得:△ABC是等边三角形,
∴∠B=∠C=60°,
∵FM⊥BC,
∴∠BFM=30°,
∴BM=![]() BF=
BF=![]() CD,
CD,
∴BM=![]() BC=
BC=![]() ,
,
∴M与D重合,
∴DF⊥BC;
故答案为:![]()

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目






