Question

【题目】如图，已知A，B两点在直线1的同侧，点A′与A关于直线l对称，连接A′B交l于点P．若A′B=a。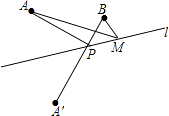

（1）求AP+PB。
（2）若点M是直线l上异于点P的任意一点，求证：AM+MB＞AP+PB。

Answer 1

【答案】
（1）解：∵点A′与A关于直线l对称，∴PA=PA′
∴PA+PB=PA′+PB=A′B=a
（2）解：∵点A′与A关于直线l对称，∴MA=MA′
∴AM+BM=MA′+MB
由（1）可知：AP+PB=A′B
由两点之间线段最短可知：MA′+MB＞A′B，即AM+MB＞AP+PB
【解析】（1）轴对称的性质有：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线 ， 线段的垂直平分线上的点与这条线段的两个端点的距离相等。根据性质可得PA+PB=PA′+PB=A′B=a。
（2）根据性质有MA=MA′，所以AM+BM=MA′+MB，由（1）可知：AP+PB=A′B，根据两点之间线段最短可得结论。