题目内容
如图,在正方形ABCD中,E是CD边上的中点,AC与BE相交于点F,连接DF.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角). 
1.(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形;
2.连接AE,试判断AE与DF的位置关系,并证明你的结论;
3.延长DF交BC于点M,试判断BM与MC的数量关系,并说明理由。
【答案】
1.答:△ABC≌△ADC,△ABF≌△ADF,△ BCF≌△DCF;
2.答:AE⊥DF。可证△BCF≌△DCF得∠CBF=∠CDF,再证△ADE≌△BCE得∠DAE=∠CBE,故∠DAE=∠CDF,又∠DAE+∠AED=90°,所以∠CDF +∠AED=90°故AE⊥DF。
3.答:BM=MC。理由如下:可证△DCM≌△BCE,得CE=CM,又CE=CD/2,CD=BC,故CM=BC/2,即BM=MC。
【解析】略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
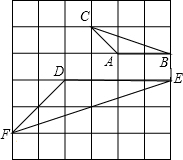 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.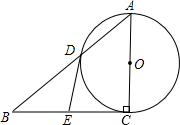 ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.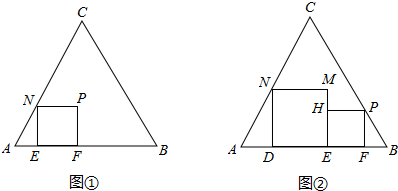
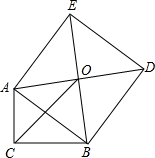 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6