题目内容
【题目】(本小题满分7分)完成下列各题:
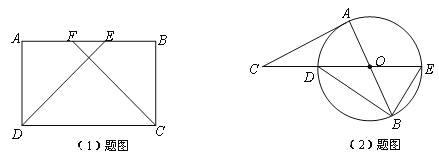
(1)如图,在矩形![]() 中,AF=BE. 求证:DE=CF;
中,AF=BE. 求证:DE=CF;
(2)如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点A. 连接
相切于点A. 连接![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() 连接
连接![]() ,
,![]() ,
,![]() 求
求![]() 的度数.
的度数.
【答案】(1)证明见解析;(2)40°.
【解析】
试题分析:(1)要证明DE=CF,只要证明△ADE≌△BCF即可.根据全等三角形的判定定理,可以得出结论.
(2)(2)先求出∠EBO,再利用同弧所对的圆心角等于圆周角的2倍,可求出∠AOC,从而求出∠C的度数.
试题解析:(1)∵矩形ABCD,
∴∠A=∠B、AD=BC,
∵AF=BE,
∴AE=BF,
在△ADE与△BCF中,
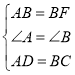 ,
,
∴△ADE≌△BCF(SAS).
∴DE=CF;
(2)(2)∵AC是⊙O的切线,
∴∠CAO=90°.
又∠AOC=2∠ABD=50°,
∴∠C=180°﹣∠AOC﹣∠CAO=180°﹣50°﹣90°=40°.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目