Question

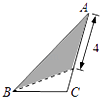
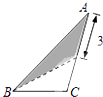
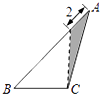
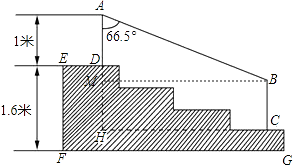
【题目】某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为1.6米，现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC（杆子的底端分别为D，C），且∠DAB=66.5°．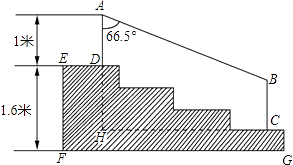
（1）求点D与点C的高度差DH；
（2）求所用不锈钢材料的总长度l．（即AD+AB+BC，结果精确到0.1米） （参考数据：sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30）

Answer 1

【答案】
（1）解：DH=1.6× =1.2（米）
（2）解：过B作BM⊥AH于M，则四边形BCHM是矩形．

∴MH=BC=1

∴AM=AH﹣MH=1+1.2﹣1=1.2．

在Rt△AMB中，∠A=66.5°．

∴AB= （米）．

∴l=AD+AB+BC≈1+3.0+1=5.0（米）．

答：点D与点C的高度差DH为1.2米；所用不锈钢材料的总长度约为5.0米．

【解析】（1）已知看台有四个台阶组成，由图可看出DH由三个台阶组成，看台的总高度已知，则DH的长不难求得；（2）过B作BM⊥AH于M，则四边形BCHM是矩形，从而得到BC=MH，再利用三角函数可求得AD，AB的长．那么所用不锈钢材料的总长度l就不难得到了．
【考点精析】本题主要考查了关于坡度坡角问题的相关知识点，需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA才能正确解答此题．