��Ŀ����
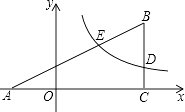
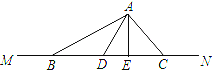
����Ŀ����ͼ��MN��һ����������ı�ֱ�Ĺ�·��C��λ�ڸù�·�ϵ�һ����������Ϊ9m��С����BD��ʻ�ڸù�·��С��λ�ڵ�A���۲�С������ijʱ�������ֳ�ͷD����βB������C�ֱ������10m��17m��2![]() m
m
��1������A��MN�����ߣ�����ΪE�������ù��ɶ����ֱ��ҳ��߶�AE��DE��AE��BE֮���������������ϵ��
��2������һ�ʵ���ʾ�£���������������⣺
�����߶�DE�ij��ȣ�
����С�����ij�ͷD�������C���ж���m��
���𰸡���1��289��2����6��2��16
��������
��1���й��ɶ������ɵó�AE��DE��AE��BE֮���������������ϵ��
��2���ɣ�1������ʽ����ã�BE2��DE2=189�Ƴ�BD=BE��DE=9��BE+DE=BD+DE+DE=9+2DE��
���Ƴ�BE2��DE2=��BE+DE����BE��DE��=9��9+2DE��=189�����DE��
�����ù��ɶ������AE,���������С�����ij�ͷD�������C���ж���m.
��1����ֱ�ǡ�ADE�У��ߡ�AED=90�㣬AD=10��
��AE2+DE2=AD2=100��
��ֱ����ABE�У��ߡ�AEB=90�㣬AB=17��
��AE2+BE2=AB2=289��
��2������ʽ������ã�BE2��DE2=189��
��BD=BE��DE=9��BE+DE=BD+DE+DE=9+2DE��
��BE2��DE2=��BE+DE����BE��DE��=9��9+2DE��=189��
��DE=6��
����ֱ����ADE�У��ߡ�AED=90�㣬
��AE= ![]() =8��
=8��
��Rt��AEC��CE= ![]() =10��
=10��
��CD=CE+DE=16��

����Ŀ��ijУ���꼶Ϊ����ѧϰ��ȤС�飬�����ġ���ѧ��Ӣ���������ѧ��˼��Ʒ�¡���ʷ���ۺϹ��˸���Ŀ��ϲ����������ʾ����飨ÿ��ֻѡһ����±��������ȡ����ѧ�����ʾ�����ͳ�ƵĽ����
��Ŀ | ���� | ��ѧ | Ӣ�� | ���� | ��ѧ | ˼��Ʒ�� | ��ʷ | �ۺ� |
���� | 6 | 10 | 11 | 12 | 10 | 9 | 8 | 14 |

���ݱ�����Ϣ������������⣺
��1�������������ѧ�������ˣ�
��2�������������ѧ���У�ϲ����Ŀ��������ࣻ
��3�������ϱ��е����ݲ�ȫ����ͳ��ͼ��
��4�������У���꼶��600��ѧ������ô���Ƹ�У���꼶ϲ���ۺϿ�Ŀ��ѧ���ж����ˣ�