题目内容
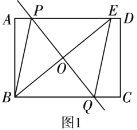
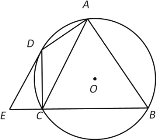
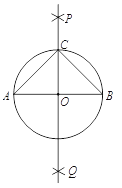
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
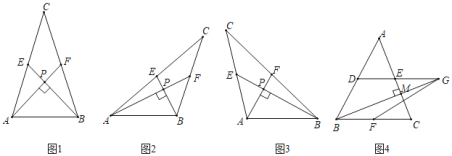
(1)如图1,当∠PAB=45°,AB=6![]() 时,AC= ,BC= ;如图2,当sin∠PAB=
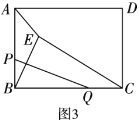
时,AC= ,BC= ;如图2,当sin∠PAB=![]() ,AB=4时,AC= ,BC= ;
,AB=4时,AC= ,BC= ;
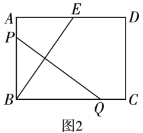
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
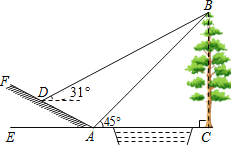
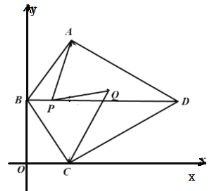
(3)如图4,在△ABC中,AB=4![]() ,BC=2
,BC=2![]() ,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至G,使得GE=DE,连结BG,当BG⊥AC于点M时,求GF的长.
【答案】(1)6![]() ,6
,6![]() ,2
,2![]() ,2
,2![]() ;(2)AC2+BC2=5AB2,见解析;(3)GF=
;(2)AC2+BC2=5AB2,见解析;(3)GF=![]()
【解析】
(1)如图1,由等腰直角三角形的性质得到AP=BP=6,根据三角形中位线的性质和平行线分线段成比例定理可得PE=PF=3,利用勾股定理可得AC和BC的长;如图2,根据特殊三角函数值可得∠BAP=30°,计算PB和AP的长,同理由中线的性质和勾股定理可得结论;
(2)设PF=m,PE=n则AP=2m,PB=2n,根据勾股定理分别列等式,可得结论;
(3)如图4,作辅助线,证明四边形EFCG是平行四边形,得Q是FG的中点,根据中垂三角形的定义可知:△FCG是中垂三角形,利用(2)中三边的关系可得GF的长.
(1)解:如图1,∵AF⊥BE,
∴∠APB=∠APE=∠BPF=90°,
∵∠PAB=45°,AB=6![]() ,
,
∴AP=PB=6,
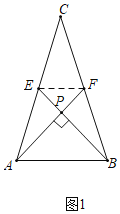
如图1,连接EF,
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EF=![]() AB,
AB,
∴![]() ,
,
∴PE=PF=3,
由勾股定理得:AE=BF=![]() =
=![]() =3
=3![]() ,
,
∴AC=BC=2AE=6![]() ,
,
如图2,∵sin∠PAB=![]() ,AB=4,AF⊥BE,
,AB=4,AF⊥BE,
∴∠PAB=30°,
∴BP=![]() AB=2,AP=2
AB=2,AP=2![]() ,
,
∵AF、BE是△ABC的中线,
∴PE=![]() PB=1,PF=
PB=1,PF=![]() AP=
AP=![]() ,
,
由勾股定理得:AE=![]() =
=![]() =
=![]() ,
,
BF=![]() =
=![]() =
=![]() ,
,
∴AC=2AE=2![]() ,BC=2BF=2
,BC=2BF=2![]() ,
,
故答案为:6![]() ,6
,6![]() ,2
,2![]() ,2
,2![]() ;
;
(2)解:猜想:AB2、BC2、AC2三者之间的关系是:AC2+BC2=5AB2,
证明:如图3,设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=AB2①,
在Rt△APE中,(2m)2+n2=(![]() )2②,
)2②,
在Rt△BPF中,m2+(2n)2=(![]() )2③,
)2③,
由①得:m2+n2=![]() ,由②+③得:5( m2+n2)=
,由②+③得:5( m2+n2)=![]() ,
,
∴AC2+BC2=5AB2;
(3)解:如图4,连接CG,EF,过点F作FN∥BG交CG于点N,FG与AC交于点Q,
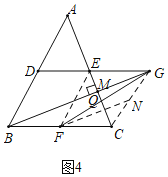
∵FN∥BG,BG⊥AC,
∴FN⊥AC,
∵F是BC的中点,
∴N是CG的中点,
∵D、E分别是AB、AC的中点,
∴DE=FC,DE∥FC,
∵ED=EG,
∴EG=FC,EG∥FC,
∴四边形EFCG是平行四边形,
∴Q是FG的中点,
∴△FCG是中垂三角形,
∵AB=4![]() ,BC=2
,BC=2![]() ,
,
∴CG=EF=BD=2![]() ,FC=
,FC=![]() ,
,
由(2)中结论可知:5FC2=CG2+FG2,
即5×5=(2![]() )2+FG2,
)2+FG2,
∴GF=![]() .
.

【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)