Question

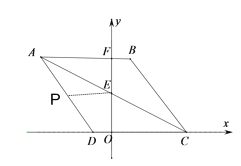
【题目】如图，O为坐标原点，四边形ABCD是菱形，A(-4，4)，B点在第一象限，AB=5，AB与y轴交于点F，对角线AC交y轴于点E.

(1)直接写出B点C点坐标；

(2)动点P从C点出发以每秒1个单位的速度沿折线段C—D—A运动，求△EDP的面积y与时间t的关系式

(3)在(2)的条件下，是否存在一点P，使△APE沿其一边翻折构成的四边形是菱形，若存在，求出点P坐标；若不存在，请说明理由.

Answer 1

【答案】(1)B(1，4)，C(4，0)；(2)y=5-t(0≤t<5)，y=t-5(5<t≤10)；(3)存在，P(-2.5，2)或P(-4，)

【解析】

（1）根据A点坐标和AB=5可得B点坐标，过点B作BG⊥OC，求出GC即可得到C点坐标；

（2）过点E作EN⊥BC于点N，延长EN交AD于M，所以MN⊥AD，根据菱形的性质可得OE=EN，OC=CN=4，在Rt△BNE和Rt△BFE中，通过勾股定理构建方程求出OE=EF=ME=2，然后根据三角形面积公式列式即可；

（3）分两种情况：①点P在DA上，且AP=AE时，沿PE翻折,可得四边形为菱形，此时可根据相似三角形的性质求出PR，DR，从而得到P点坐标；②当P在DA上，且AP=PE时，沿AE翻折,可得四边形为菱形，此时PE为△ADC的中位线，根据中点坐标公式可求出P点坐标.

解:(1)∵A(-4，4),AB=5，四边形ABCD是菱形，

∴B (1，4),BF=1，

过点B作BG⊥OC，则BG=4，BC=5，

∴GC=3，

∴C(4,0)

（2）过点E作EN⊥BC于点N，延长EN交AD于M，所以MN⊥AD，

∵四边形ABCD是菱形，∴∠DCA=∠BCA，

∴OE=EN，

由（1）知OC=4，∴CN=4，BN=1，

设OE=x，则OE=EN=x，EF=4-x，

在Rt△BNE中，BE2=x2+1，在Rt△BFE中，BE2=(4-x)2+1，

∴x2+1=(4-x)2+1，解得：x=2，即OE=2，EF=2，

∴ME=EF=2，

∴当点P在CD上时，y=，

当点P在DA上时，y=，

（3）①如图：点P在DA上，且AP=AE时，沿PE翻折,可得四边形为菱形，

作AQ⊥OQ，PR⊥OQ，由（1）（2）可得OD=1，EF=2,AF=4，

根据勾股定理可得：AP=AE=，∴PD=5-，

易得△PRD∽△AQD，∴，

∴PR=4-，DR=3-，∴OR=4-，

∴此时P点坐标为（）；

②如图：当P在DA上，且AP=PE时，沿AE翻折,可得四边形为菱形，

∵AP=PE，∴∠PAE=∠PEA，

又∵∠PAE=∠EAF，

∴∠PEA=∠EAF，

∴AF∥PE∥CD，

由（1）（2）可知E为AC中点，∴P为AD中点，

∵A（-4,4），D（-1,0），

∴P（）

综上所述：满足题意的P点坐标为（）或（）.