题目内容
【题目】已知,如图,将∠D=60°的菱形ABCD沿对角线AC剪开,将△ADC沿射线DC方向平移,得到△BCE. 点M为BC边上一点(点M不与点B、点C重合),将射线AM绕点A逆时针旋转60°,与EB的延长线交于点N,连接MN.
(1)求证:∠ANB=∠AMC;
(2)探究△AMN的形状,并说明理由.
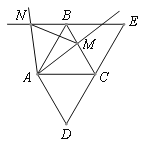
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)①先由菱形可知四边相等,再由∠D=60°得等边△ADC和等边△ABC,则对角线AC与四边都相等,利用ASA证明△ANB≌△AMC,得结论;
②根据有一个角是60°的等腰三角形是等边三角形得出:△AMN是等边三角形;
试题解析:(1)∵ABCD为菱形,
∴AB=AD=CD=BC,
又∵∠D=60°,
∴△ADC为等边三角形,
∴∠DAC=60°,AC=AD,
∴AC=AB=BC,
又∵△BCE≌△ADC,∠CBE=∠DAC=60°,
∴∠CBN=120°
∵∠ANB=360°-∠CBN-∠MAN-∠BMA=180°-∠BMA,∠AMC=180°-∠BMA
∴∠ANB=∠AMC.
(2)∵AC=AB=BC,
∴△ABC为等边三角形,
∴∠BAC=60°.
∵∠MAN=60°,
∴∠MAN=∠BAC,
∴∠MAN-∠BAM=∠BAC-∠BAM,即∠BAN=∠CAM,
又∵∠ANB=∠AMC,AB=AC,
∴△BAN≌△CAM,
∴AN=AM,
∵∠MAN=60°,
∴△AMN为等边三角形.

练习册系列答案
相关题目